These html pages are based on the
PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also
more information and a PDF version available.
Chapter 2
Discontinuous Galerkin discretization
With the continuity equation given in its continuous form (1.5), solving this system of
equations analytically has been accomplished only for special cases so far. Those special
cases are e.g. one-dimensional simplifications and particular initial as well as boundary
conditions [SES06,Syn91]. Therefore, we have to solve these equations numerically by discretization of
the continuous form of the continuity equation.
Several approaches exist to solve such a system of equations numerically. Here, we give a
short overview of the most important ones with an Eulerian [Lam32] approach in spatial
domain:
- Finite differences belong to one of the most traditional methods. They approximate the
spatial derivatives by computing derivatives based on particular points in the simulation
domain. Following this approach, conserved quantities are given per point.
- Classical finite elements methods (FEM) discretize the equations based on an overlapping
support of basis functions of disjunct cells. This leads to continuous approximated
solutions at the cell boundaries. However, continuous finite element methods suffer from
complex stencils with access patterns over several cells.
- With the Discontinuous Galerkin finite elements method (DG-FEM), a similar approach
as for the classical FEM is taken. However, the basis functions are chosen in a way that
their support is cell-local. On the one hand, this avoids complex access patterns, whereas
on the other hand, this generates discontinuities at cell borders requiring solvers for the
so called Riemann problem. Finite volume simulations can be interpreted as a special case
of the DG-FEM formulation with a single basis function of 0-th order.
With our main focus on wave-propagation dominated problems and the DG-FEM being well-suited
to solve such problems (see e.g. [LeV02,HW08,Coc98]), we continue studying the discretization of the
continuity equation for the remainder of this thesis with the DG-FEM. To determine the framework
requirements to run such DG-FEM simulations on dynamic adaptive grids, a basic introduction to the
discretization and approximations of the solution in each grid cell is required and given in the next
sections.
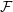
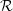 and
and