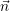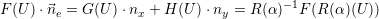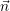These html pages are based on the
PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also
more information and a PDF version available.
2.9 Rotational invariancy and edge space
Working with triangles, a straightforward evaluation of the term F(Ui(t)) ⋅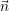 (x,y) involving both flux
functions G(U) and H(U) followed by a multiplication with the outward pointing normal can be
optimized. We use the so-called rotational invariancy [Tor01], with flux functions for the hyperbolic
systems considered in this thesis holding a crucial property.
(x,y) involving both flux
functions G(U) and H(U) followed by a multiplication with the outward pointing normal can be
optimized. We use the so-called rotational invariancy [Tor01], with flux functions for the hyperbolic
systems considered in this thesis holding a crucial property.
We consider a two-dimensional normal vector 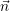 e = (cos(α),sin(α))T pointing outward the edge e.
Then, for the computation of the flux update, the equation
e = (cos(α),sin(α))T pointing outward the edge e.
Then, for the computation of the flux update, the equation
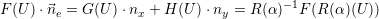 | (2.13) |
holds true for a given rotation matrix R(α). The matrix is setup with an n-dimensional rotation
matrix with the entries stored to the n×n direction dependent components such as the velocity and
momentums and 1 on the diagonal for direction independent components. This matrix rotates, e.g.,
orientation-dependent components such as the velocity and momentum which are parallel to 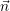 e to the
x-axis (see Appendix A.1.7 for an example).
e to the
x-axis (see Appendix A.1.7 for an example).
For later purpose, the right hand side of Equation (2.13) is further described:
-
1.
- To compute the flux across an edge, the conserved quantities depending on a direction are
first rotated from the reference space to the so-called edge space [AS98].
-
2.
- Then, the change of conserved quantities is evaluated in the one-dimensional edge space.
-
3.
- Finally, the updates related to the flux are rotated back to reference space and applied to
the conserved quantities stored in the reference space.
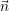 (x,y) involving both flux
functions G(U) and H(U) followed by a multiplication with the outward pointing normal can be
optimized. We use the so-called rotational invariancy [Tor01], with flux functions for the hyperbolic
systems considered in this thesis holding a crucial property.
(x,y) involving both flux
functions G(U) and H(U) followed by a multiplication with the outward pointing normal can be
optimized. We use the so-called rotational invariancy [Tor01], with flux functions for the hyperbolic
systems considered in this thesis holding a crucial property.