2.1 Grid generation

To store our simulation data at spatially related positions, we require a grid-generation strategy which decomposes the domain into non-overlapping cells. Relevant simulation data can then be stored on each grid cell and at hyperfaces separating the grid cells. The most commonly used cell-wise grid generation for DG simulations on two-dimensional domains are Cartesian, Voronoi and triangular ones:

(a)

A Cartesian two-dimensional grid generation results in cells with edges parallel to the basis vectors of a Cartesian coordinate system. Using such a structured grid, direct access of the neighboring cells can lead to more efficient access of data in adjacent cells. However, due to refinement of the grid in particular areas, hanging nodes are created (see [BL98] for AMRClaw) and have to be handled in a special manner which is typically based on explicit knowledge of the developer (cf.  [BHK07,MNN11]).

(b)

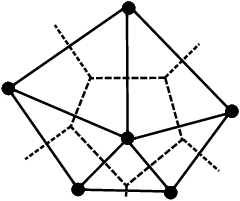
Simulations executed on grids generated by Voronoi diagrams (e.g.  [Wel09, Ju07], see dashed lines in Fig. 2.1) provide an alternative meshing, but make computations with higher-order methods challenging due to the manifolds (e.g. different number of corners) of different shapes.

---

Figure 2.1: Voronoi grid-based generation (dashed line) and the corresponding triangle-based grid generation (solid lines). See e.g.  [Ju07] for information about generation.

---

(c)

Using triangular grids for simulations, this yields two major beneficial components: First, there is a duality between triangular grids generated by Delaunay triangulation and Voronoi diagrams [She02,DZM07] as shown in Fig. 2.1. Thus, using a triangular grid would also allow us to use it as a grid created by a Voronoi diagram algorithm. Second, adaptive Cartesian grid generation leads to hanging nodes. These nodes can be avoided by inserting additional edges. However, this also requires interfaces provided by the simulation developer. Using adaptive triangular grids based on bisection of the triangle, such hanging nodes can be directly avoided by inserting additional edges.

Due to the hanging nodes created by Cartesian-aligned grids and the very common usage of triangular grids for two-dimensional DG-FEM (cf. [HW08,AS98]), we decided to use a triangulation of our simulation domain.