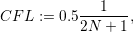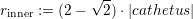
Using an explicit time-stepping scheme, the size of a time step to run a stable simulation must not exceed a particular value. We use the Courant-Friedrichs-Lewy (CFL) [CFL28] condition which relates the maximum time-step size in each cell to its shape and size as well as the wave propagation speed in the cell.
Several methods for advancing the simulation in time can then be used, each one different in the number of cells being advanced with the same time-step size: Cell-local [HW08], patch-wise [BGLM11], cluster-based [CKT09] and global time stepping methods with the cluster-based one not yet existing for dynamically adaptive grids. We decided to implement the global time stepping method with the same integration width over time for all cells.
Considering isosceles triangles, the cell size and shape dependent factor is computed with the in-circle radius
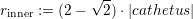
The propagation speed of the wave itself depends on the solution computed for the Riemann problem. For flux solvers based on linearization of the flux function (see Sec. 1.2.1, 1.2.2), this wave propagation speed s
waveisgivenbytheeigenvaluesoftheJacobianofthelinearizedfluxfunction.ForourRusanovflux,thispropagationspeedisequaltotheviscosityparameterν. This yields
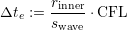 | (2.28) |
for all time-step sizes Δte based on the flux computations on all cell edges e with the CFL set to a constant value depending on the maximum degree of basis functions and the used flux solver. For basis functions of degree N, we set this value to