These html pages are based on the PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also more information and a PDF version available.

[next] [prev] [prev-tail] [tail] [up]

2.5 Mass matrix M

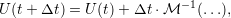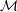
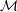
Discretizing the time step term from Eq. (2.9). We can factor out U by considering that φ are functions only depending on spatial parameters. This yields

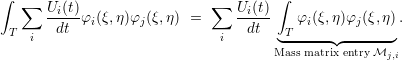∫ ∑ ∑ ∫ Ui(t)φi(ξ,η)φj(ξ,η ) = Ui(t) φi(ξ,η)φj(ξ,η). T i dt i dt ◟T-----◝◜------◞ Mass matrix entry Mj,i
(2.10)

The integrals on the right-hand side of Eq. (2.10) can then be precomputed and their values stored to the mass matrix 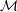M. Using vector notation 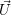U⃗, we get a matrix-vector formulation

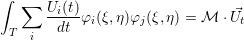∫ ∑ Ui(t) ⃗ T dt φi(ξ,η )φj (ξ,η) = M ⋅Ut i
(2.11)

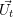with U⃗t also a matrix in case of several conserved quantities.

See Appendix A.1 for examples of matrices derived in this section and used in our simulations. Those matrices are computed with Maple1 , a computer algebra system for symbolic computations.

Applying the explicit Euler time-stepping method, this can then be rearranged to

U(t+ Δt ) = U(t)+ Δt ⋅M -1(...),
thus requiring the computation of the inverse of the mass matrix (see Section A.1.3 for examples). Higher-order integration in time is further discussed in Sec. 2.14.

[next] [prev] [prev-tail] [front] [up]