These html pages are based on the PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also more information and a PDF version available.

[next] [prev] [prev-tail] [tail] [up]

2.2 Triangle reference and world space

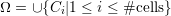
The entire simulation domain can be represented by a set of triangles

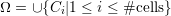
Ω = ∪ {Ci|1 ≤ i ≤ #cells}
with triangle cell primitives Ci only overlapping at their boundaries. Dropping the subindex i, each cell area is given with
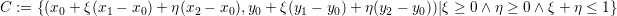
C := {(x0 + ξ(x1 - x0) + η(x2 - x0 ),y0 + ξ(y1 - y0)+ η(y2 - y0))|ξ ≥ 0∧ η ≥ 0∧ ξ + η ≤ 1}
and (xn,yn) referring to one of the three vertices of the triangle C, see Fig. 2.2 for an example. We refer to the space of the coordinates (x,y) as world space, whereas (ξ,η) are coordinates in reference space.

pict

Figure 2.2: Triangular cell Ci in world space.

By applying affine transformations, each triangle Ci and the conserved quantities can be mapped from world space to a so-called reference triangle. For the sake of clarity, the formulae in the following sections are given relative to such a reference triangle.

pict

Figure 2.3: Triangle reference space with isosceles triangle

We use the triangle reference space with both triangle legs of a length of 1 and aligned at the x- and y-axes, see Fig. 2.3. The support in reference space is then given by

T = {(ξ,η) ∈ [0,1]2 | ξ ≥ 0 ∧η ≥ 0 ∧ ξ + η ≤ 1}. (2.1)

Using a homogeneous point representation, mappings of points from reference to world space are achieved with

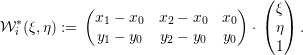
( ) ( ξ) W *(ξ,η) := x1 - x0 x2 - x0 x0 ⋅ (η ) . i y1 - y0 y2 - y0 y0 1

Assuming a mathematical formulation which is independent of the spatial position of the triangle, we can drop the orientation-related components and simplify this mapping to

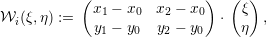
( ) ( ) x1 - x0 x2 - x0 ξ Wi (ξ,η) := y1 - y0 y2 - y0 ⋅ η ,
by defining one of the triangle’s vertices as the world space origin. Only considering the matrix formulation, this is more commonly known as the Jacobian
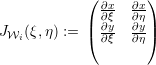( ∂x ∂x) | ∂∂ξy ∂∂ηy| JWi (ξ,η) := ( ∂ξ ∂η)
(2.2)

computing the derivatives in world space with respect to reference space coordinates (ξ,η). Affine transformations to and from world space can then be accomplished by additional projections of particular terms (see [AS98,HW08]) and for our simulations on the sphere in Section 6.5.

With the points

e′(w ) := (1 - w,w ), 1′ e2′(w ) := (0,1 - w),and (2.3) e3(w ) := (w, 0)
parameterized with w, the interval for each edge is given by ei := {e′i(w)|w ∈ [0,1]}. Note the unique anti-clockwise movements of the points e′i(w) for all edges and a growing parameter w which is important for the unique storage order of quantities at edges.

For the remainder of this chapter, we stick to the world-space coordinates.

[next] [prev] [prev-tail] [front] [up]