These html pages are based on the PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also more information and a PDF version available.

[prev] [prev-tail] [tail] [up]

2.14 Time stepping schemes

Regarding the derivative of our conserved quantities with respect to time, we only considered the explicit Euler method which is of first order. This section is about higher-order Runge-Kutta time stepping schemes and sets up the basic requirements of the integration of our simulation in time. For sake of readability, the spatial parameters ξ and η for the conserved quantities are dropped in this section.

Typical higher-order time stepping methods such as Runge-Kutta (RK) are a commonly chosen alternative to the explicit Euler due to their higher accuracy in time. Regarding our requirement analysis, such higher-order methods should be obviously be considered in our development.

With the RK method, accuracy of higher-order is achieved combining the conserved quantity updates based on several smaller time-step computations. A generalization of the RK method for higher-order time integration leads to s stages i = (1,2,…,s) [But64,CS01,HW08]:

V0 := U (t); V := V + Δt ∑s a D ; i 0 j=1 i,j j (2.29) Di := R(Vi);
yielding an explicit formulation for ai,j = 0 for i < j. The solution is finally given by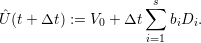
s ˆU(t+ Δt ) := V + Δt ∑ b D . 0 i=1 i i

Considering the framework development in Part III, we store both update values Di and conserved quantities V i for each stage and finally update the conserved quantities by the formula given with ai,j and bi. The coefficients ai,j and bi depend on the desired order of the method and are typically given in the format of the Butcher tableau [But64] (See Appendix A.1.6).

[prev] [prev-tail] [front] [up]