These html pages are based on the PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also more information and a PDF version available.

[next] [prev] [prev-tail] [tail] [up]

2.6 Stiffness matrices S

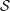
For a partial evaluation of the stiffness terms, we follow the direct approach of expanding the approximated solution, yielding

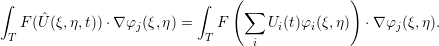
( ) ∫ ∫ ∑ F (Uˆ(ξ,η,t)) ⋅∇ φj(ξ,η ) = F Ui(t)φi(ξ,η) ⋅∇ φj(ξ,η). T T i

Since an accurate integration for flux functions with rational terms would be computationally infeasible, approximations are typically used for this evaluation [Coc98,HW08,Sch03]. Such an approximation is the nodal-wise evaluation of the flux term at nodal points and reconstruction of a continuous function with the basis functions φi(ξ,η). This simplifies our stiffness term to

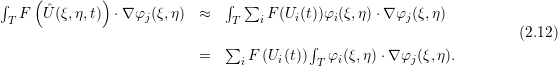
∫ ( ˆ ) ∫ ∑ T F U (ξ,η,t) ⋅∇ φj(ξ,η) ≈ T iF(Ui(t))φi(ξ,η) ⋅∇φj (ξ,η) ∫ (2.12) = ∑i F (Ui(t)) φi(ξ,η)⋅∇ φj(ξ,η). T

For the modal basis function, a projection to/from nodal basis is required. We continue by replacing F with two flux functions G and H (see Section 1.1). Then, we can again evaluate integrals and rearrange the equations to a matrix-matrix formulation

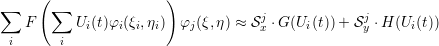
∑ ( ∑ ) F Ui(t)φi(ξi,ηi) φj(ξ,η) ≈ Sj ⋅G(Ui(t))+ Sj ⋅H (Ui(t)) i i x y
with Sj selecting the j-th row of matrix S (see Appendix A.1.4).

[next] [prev] [prev-tail] [front] [up]