Stack- and stream-based simulation on a static grid

These html pages are based on the PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also more information and a PDF version available.

[next] [prev] [prev-tail] [tail] [up]

4.5 Stack- and stream-based simulation on a static grid

We continue with a concrete description on how we execute a stack- and stream-based simulation on a static grid. Due to the static grid, we assume the grid structure already stored in the structure stream.

4.5.1 Required stacks and streams

In order to run a simulation for solving the hyperbolic equations with our stack-based communication system, we continue determining further buffer requirements. We introduce different stack types:

Communication stacks S_lr: Two stacks are required for communication patterns via edges or vertices due to stack operations distinguishing between the left and right side of the SFC.
Buffer stack S_t: This stack is used for semi-persistent data, e.g. to store edge communication data during the forward traversal and fetch it from the buffer to perform the time step integration.
Traversal persistent stacks S_fb: Two stacks are used for forward and backward traversal direction fetching data from one stack and pushing it to the other stack.

Then, the basic stack for grid storage, usable for a pure grid traversal without any computations, is given by


Stack S	Description of purpose	Classification


S_fb^structure	Grid representation	persistent

Depending on the simulation requirements, additional stacks are used. For a simulation with a DG method on a static grid and flux computations requiring an edge-based communication, this leads to the following additional stacks:


Stack S	Description of purpose	Classification


S_fb^simCellData	Storage for cell data (e.g. DoF)	persistent

S_lr^simEdgeComm	Edge data communicated to adjacent cells	semi-persistent

S_t^{simEdgeBuffer}	Buffer for data exchange via edges	semi-persistent

The buffer S_t^{simEdgeBuffer} is required to buffer the communication data during the forward traversal. This data from adjacent cells is then fetched during the backward traversal.

4.5.2 DG simulation with stacks and streams

With our knowledge on the basics of a hyperbolic simulation, we are going to assemble a simulation with the stack- and stream-based approach introduced in the previous Sections.

For flux computations, we do not follow the approach of splitting the flux computations as suggested in [BBSV10] which basically avoids computing the flux based on the DoF on each cell’s edge. Such an approach is not applicable with the Rusanov flux solvers from Section 2.10 as well as many other solvers.

A single time step is then computed with the following algorithmic pattern using a forward and backward traversal.

Forward traversal:

(a)

Storing flux paramters: For each cell traversed along the SFC, we distinguish between edge types (see Section 4.3.2).

new: For edge types new, the DoF on an edge required for the flux evaluation are first computed (see Section 2.7) and then communicated to the cell adjacent to the edge. Due to the stack-based communication, each edge of type new is followed by a corresponding traversal of the cell adjacent to the edge.
old: For each edge type old, the previously written flux parameters are read from the communication stacks and pushed to the semi-persistent stack S_t^{simEdgeBuffer}, directly followed by a push of the cell-local edge coefficients. This operation converts non-persistent data to semi-persistent data.
boundary: In case of a boundary condition, the parameters for the flux computation are reconstructed based on the selected type of boundary condition (see Section 2.11) and are, together with the corresponding DoF of the local edge, pushed to the S_t^{simEdgeBuffer}.

Additionally to the flux parameters, the inner cell radius is also transfered for computing the CFL condition (see Section 2.13) to allow a time step size computation which depends on the inner cell radius of each cell.

Traversal-intermediate processing:

(b): Compute fluxes: After storing the cell size as well as all flux DoF consecutively on the simEdgeBuffer stack, the fluxes are evaluated and the flux updates written to the same buffer storage (see Section 2.10).
(c): Compute time-step size: Based on the flux computations, the maximum time-step size is directly derived from the CFL condition, the maximum wave speed and the cell size (see Section 2.13). The cell size, in addition to the flux parameters, has also been stored to the edge buffer stack.

Backward traversal:

(d): Receive flux updates (Section 2.7): During the backward traversal, for each edge type new, the pair of flux-updates on the shared edge is read from the buffer. The flux update associated to the currently traversed cell is then used for the time stepping and the other flux update is pushed to the communication stacks to be processed by the adjacent cell.
Flux updates for edges of type old have previously been pushed to the corresponding left or right edge communication stack and are read from the respective stack.
(e): Advance the time step on the data stored at each cell (Section 2.14): The flux-updates for each edge of a cell are available either via the edge buffer for edges of type new or via the stack system for edges of type old. Thus the cell can be advanced in time based on the flux updates and the computed time-step size.

An alternative approach for flux computations presented in the traversal-intermediate processing is computing the flux updates during the first forward traversal before pushing the flux parameters to the edge buffer (see [SBB12] for an implementation). This avoids the mid-processing and, thus, also additional bandwidth requirements; However, it does not yield the optimization of vectorized flux evaluation for finite volume simulations (see Section 4.10.4) and hence was not considered in this work.

4.5.3 Non-destructive streams

With a software concept using input- and output-streams and temporary stacks only (cf. [MRB12,Nec09,Wei09]), all the data has to be read from one memory location and written to another memory location. Among others, this results in increased cache utilization due to additional memory being accessed and additional cache blocks used. Another performance aspect are additional index computations for the second stack.

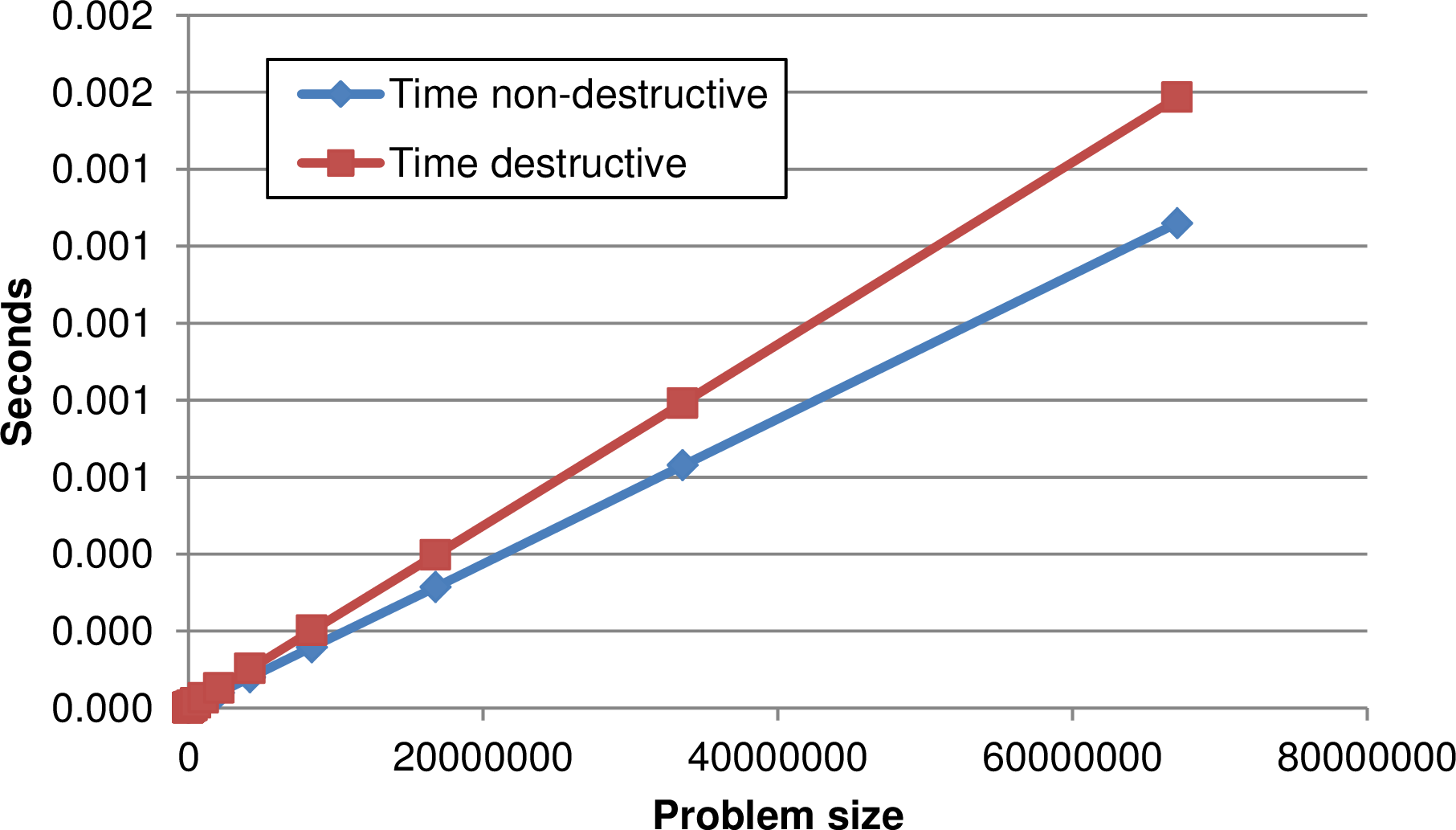
We tested this hypothesis with two different benchmarks based on an array of size n. Both benchmarks operate on an array of integers and successively increment the stored values. The first benchmark operates in-situ, reading a floating point value, incrementing it and writing the data back to the same array entry, whereas the second benchmark writes the result to an additional array.

pict pict

Figure 4.7: Benchmark for non-destructive streams vs. destructive streams with different stream sizes showing robust improvement for larger problem sizes with non-destructive streams.

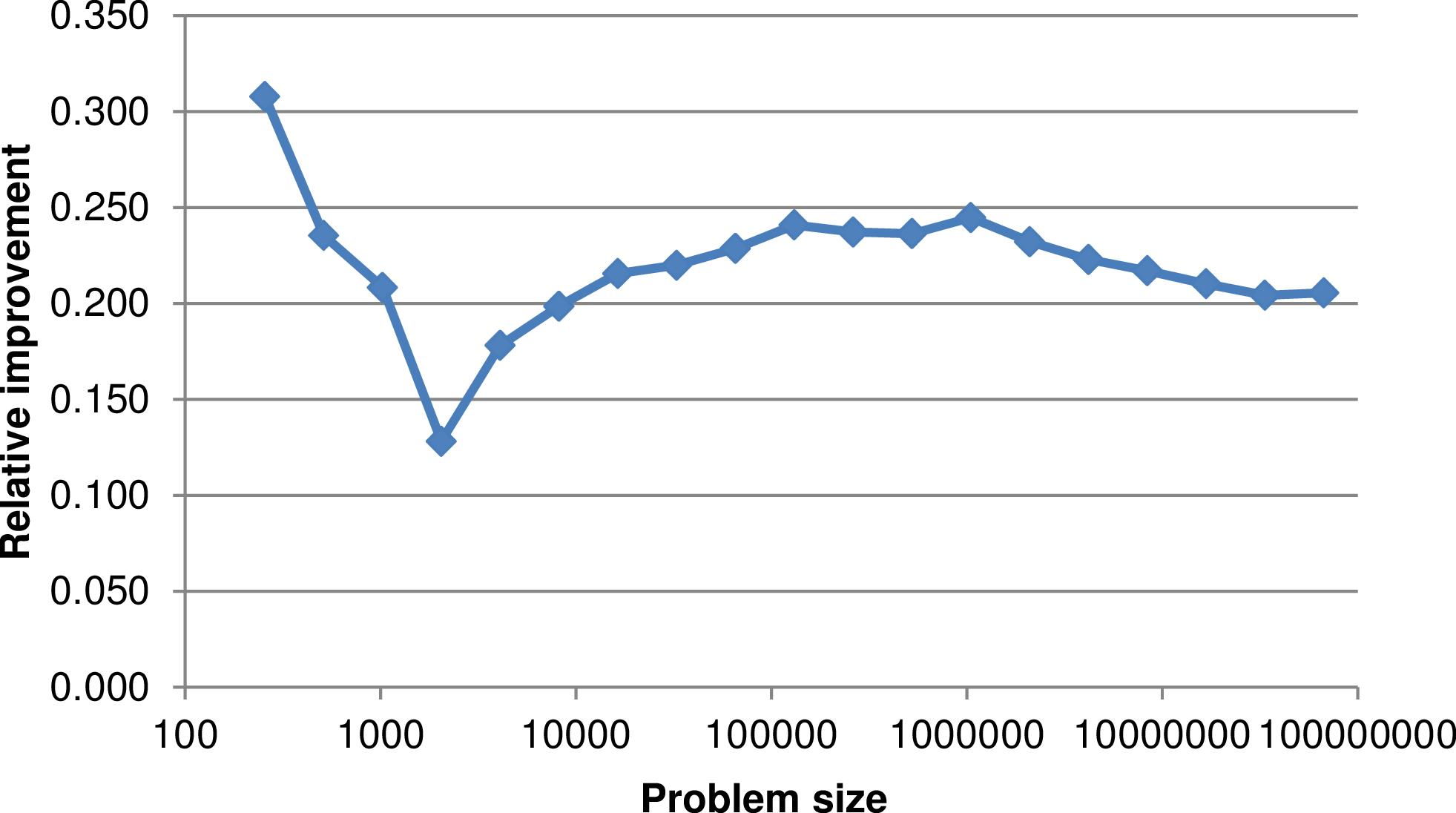
Figure 4.7 shows results for both benchmarks with different block sizes. It suggests that non-destructive streams are mandatory for memory performance. This leads to a robust performance improvement of more than 20% for larger streams using non-destructive streams.

Thus, we use an approach with non-destructive access to our stack structures and further motivate this by highlighting possible applications in our algorithm:

Avoid generation of structure stacks for reversed traversal:
Writing the structure stream to the memory with an additional memory buffer leads to increased pullution of the cache despite no changing grid. With adaptivity traversals introduced in the next section, several forward- and backward-traversals are executed obviously without requiring reconstruction of structure stacks during each traversal since the structure is fixed. Hence, we reuse the structure stacks.
In-situ cell updates for each time step:
During the forward traversal, an input/output stream would lead to obsolete copy operations of data stored per cell which does not require any modifications. Such data can be e.g. the Jacobi matrix, vertex coordinates or distorted grids.

This yields two different kinds of non-destructive streams. Assuming e.g. a grid traversal in forward direction accessing cell data, a top-down stream is used to iterate over the stack data top-down. A bottom-up stream can be used in a similar way to start iterating over the data from the very first element on the bottom of the stack. All these stream operations do not remove or add any data to stack, they only update the stack entries.

Optimizing our input/output scheme with these non-destructive streams, this modifies our stack system used for the simulation on static grids (Sec. 4.5.2) in the following way:

Forward traversal:

Structure input: top-down stream (read only (RO))
The forward structure stack is read with a non-destructive top-down stream which allows for being reused by successive traversals.
Cell data: top-down stream (RO)
The cell data is read with a non-destructive top-down stream with read access only.
Structure output: stack (write-only (WO))
The backward structure stack is cleared before the traversal and written with standard push operations to create the structure information for a backward traversal. In case of no modification of the grid structure and with the backward structure stack information already existing, we can skip creating this structure information.

Backward traversal:

Structure output: NONE
No structure output is required since the forward structure stack already exists.
Cell data: bottom-up stream (read-write (RW))
The backward structure stack is read with a non-destructive top-down stream with read-write access allowing update of cell data.
Structure input: top-down stream (RO)
The backward structure stack is read with a stream access. Since it was sucessively pushed post-order to the stack, it has to be read top-down.

We just presented the modifications of our stack system to a non-destructive system with a static grid. Next, we continue with the adaptivity traversals.

[next] [prev] [prev-tail] [front] [up]