Since our simulations require data exchange between grid cells, we describe a cache-aware way of exchanging data stored for different grid cells based on stack operations.
The high variety of possible application requirements on the grid traversals and data exchange patterns demands for a code generator. Otherwise, these variety requirements would lead to either (a) generic code including computations not required for the particularly considered application, thus wasted computation time, or to (b) handwritten code, specialized for each application which leads to code which has to be modified each time before being capable of using them for different grid traversal and communication requirements. Therefore, we decided to use a code generator and continue by introducing a structured formulation of the grid traversal and communication approach to allow the creation of the traversal code with a code generator (See Section 4.9.5). This is contrary to the approach taken before for a stack- and stream-based SFC traversal which was based only on hand-written traversal code.
We extend the grid generation approach from Section 4.1 by labeling each cell with additional information which is described in this and the next section. Such labels yield properties which are getting beneficial in upcoming Sections.

The Sierpiński SFC can be defined via a grammar [BSVB08] being recursively applied with different basic triangle traversal types given in
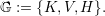 | (4.3) |
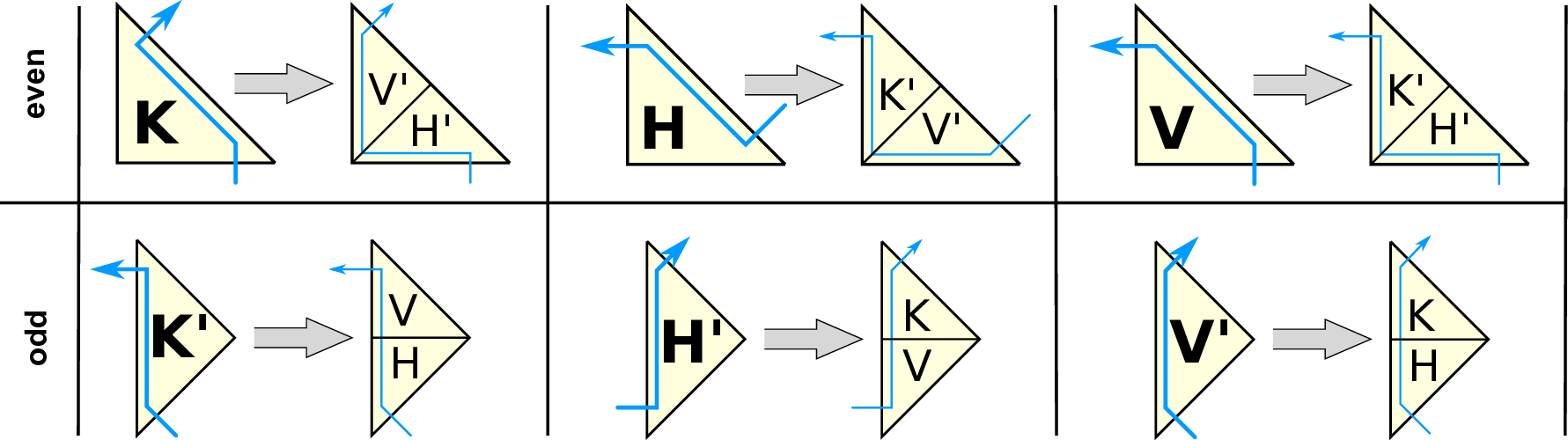
The notation of these types are related to the location of the SFC entering and leaving the triangle, see Fig. 4.2. K traversals enter a triangle via a cathetus (Kathete in German), H via the hypotenuse and V entering and leaving the triangle via a cathetus, creating a V-like shape. Additional properties are used for default and mirrored traversal by
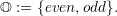 | (4.4) |
The marker odd mirrors the traversal direction along the newest vertex bisection edge. The tuple
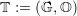 | (4.5) |
then defines all SFC traversal combinations (see Fig. 4.2 for an overview) required for our communication scheme. For visualization, we always draw the SFC close to the hypotenuse of each triangle as suggested in [Sch06].
To recursively traverse the spacetree, the function childT stores the grammar applied to the tree traversal (see cells on the right side of the gray arrow in Fig. 4.2).
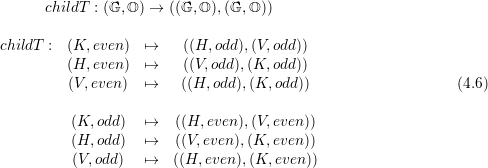
Theorem 4.3.1 (Shared edge with SFC order) The SFCs provide a unique order of the cells. This implies that each cell Ci+1 shares exactly one edge with Ci.
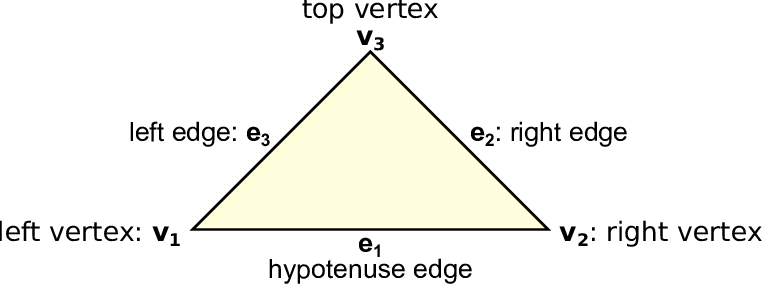
The edges of each triangle in its normalized orientation (see Fig. 4.3) are enumerated e1, e2 and e3 by starting at the hypotenuse and then enumerating the triangle legs in counter-clockwise order yielding the unique identifiers
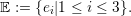 | (4.7) |
The vertices are enumerated similarly starting at the vertex left to the hypotenuse, resulting in unique identifiers
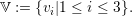 | (4.8) |
We continue with the requirements of efficient data exchange between cells. Using the Sierpiński SFC, we can exchange data among adjacent cells via pushing and fetching data to and from a stack system (see next Section).
Using such a stack-based communication demands for (a) particular access order in each cell and (b) an edge-type labeling:
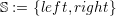
We follow the suggestion for an access order of edge and vertex primitives in [BSVB08], and write down the order in a formal way including edges ei and vertices vi with the function A : (T, S) →⋃ i∈{2,3,4}(E ∪ V)i:
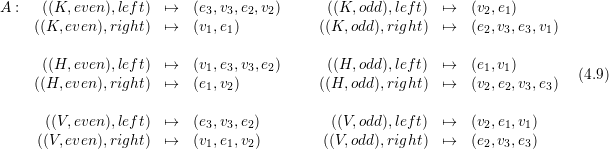
To give an example, A((K,even),left) describes the communication primitive access order of the even K triangle type (see top left image in Fig. 4.2). The access order is given by the SFC traversal direction. With the SFC drawn close to the hypotenuse, the left edge e2 is the first primitive on the left side of the SFC traversal where the SFC enters the triangle. Therefore, primitive e3 is the first one, followed by the top vertex v3 and the edge e2. Since the SFC leaves the triangle via the hypotenuse, the right vertex v2 is also on the left side of the SFC and, thus, is the last primitive regarding primitives at the left side to the SFC traversal for triangle type (K,even).
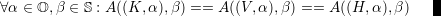
The labels for edges are then given by
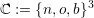 | (4.10) |
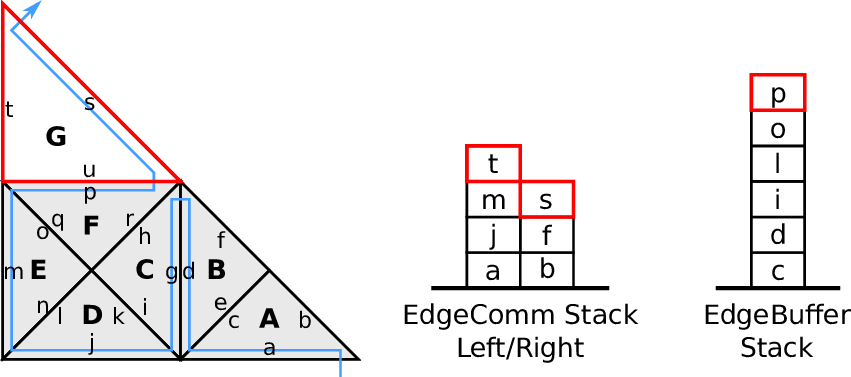
for new, old or boundary edge types on the three edges enumerated in anti-clockwise order with the enumeration starting at the hypotenuse, see Fig. 4.3. An example for labeled edges is given in Fig. 4.4. The communication itself can then be realized in a cache-aware manner based on a stack system (see Section 4.3.2).
The communication information C for the first and second child, respectively, due to cell bisection is given by
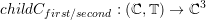
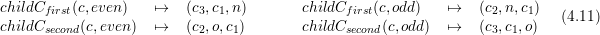
We use two stacks, the left and right communication stack which we continue to use for our edge-based communication, see e.g. [BRV12]. This communication is based on the inherited edge types and uses push and pop operations acting on stacks. A push operation is applied for edges of type new, storing new data on the stack which is to be fetched by a pop operation from another cell for the corresponding edge of type old.
With this push and pop operations to/from the respective stacks, this yields our algorithm for edge-based communication: For each traversed leaf-node, we apply push and pop operations on the left and right communication stack. The stack access is specified with our access order A : (T, S). The information whether data has to be read (pop) or written (push) to the stack is given by the edge types ℂ.
During a forward traversal, this communication scheme is able to transfer information to cells subsequently traversed by the current grid traversal. Due to this propagation direction only towards subsequently traversed cells, we require an additional backward traversal for transferring data to cells in the other traversal direction. Therefore we require a grammar with reversed access order, given by changing push and pop operations to communicate in the reversed order and also by reversing the node and edge communication order from function A.
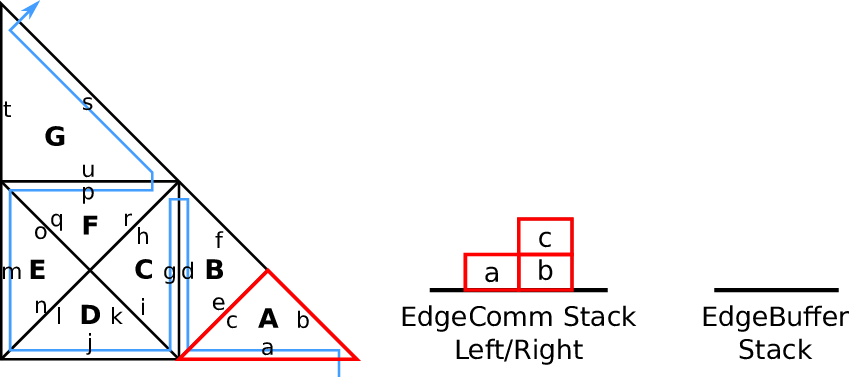
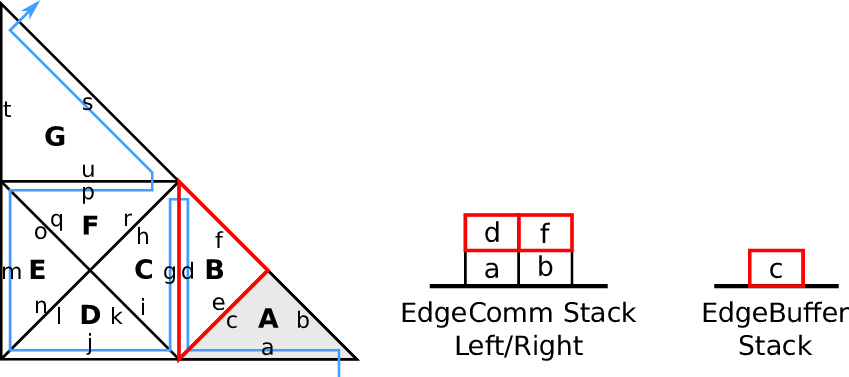
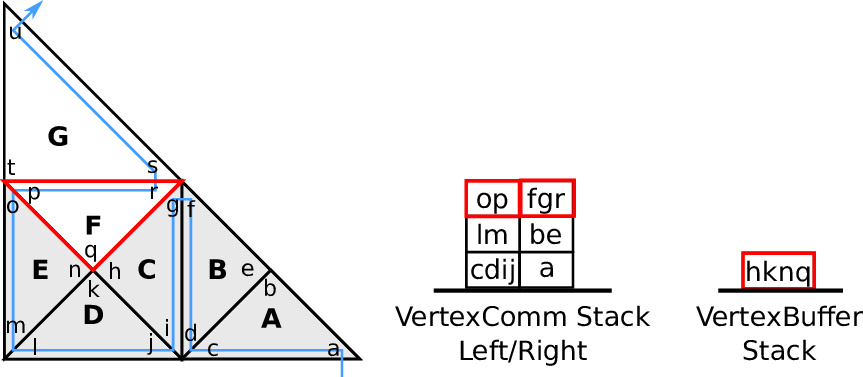
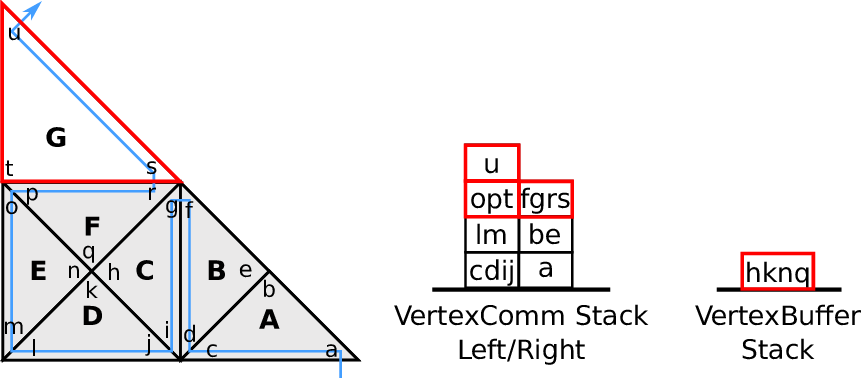
Data forwarded during the forward traversal can be either processed directly, e.g. by updating cell-local data or can be stored to an edge buffer stack with data being read from this buffer during the backward traversal. An example of the latter approach is illustrated in Fig. 4.5.
 |  |
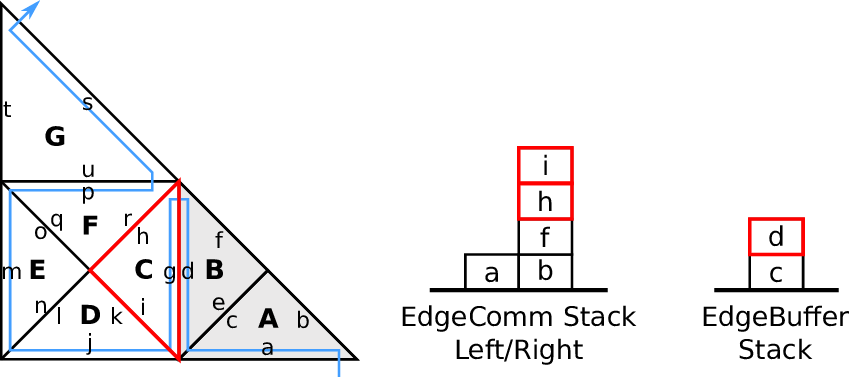 | 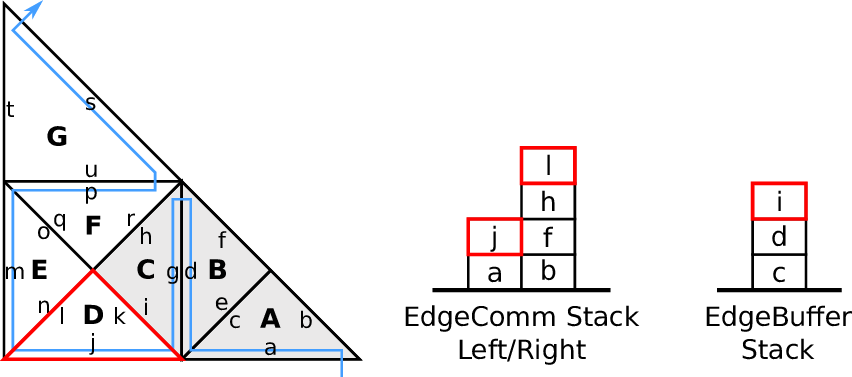 |
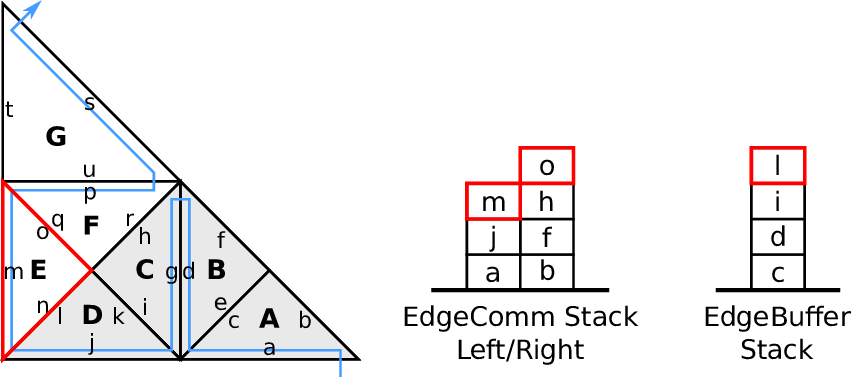 | 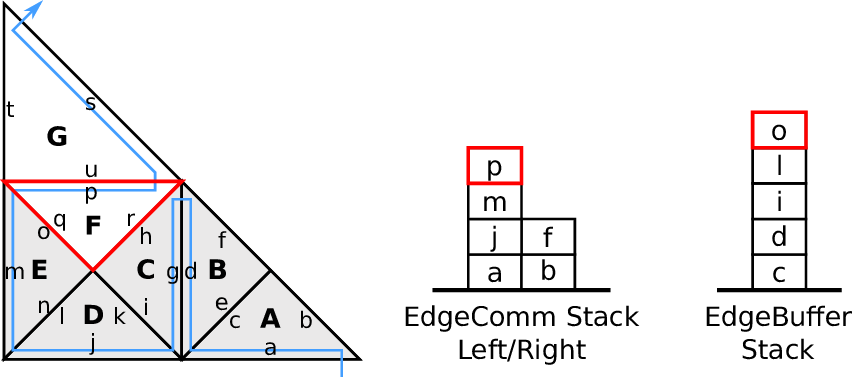 |
 |
For applications such as node-based flux limiter [KT04], finite element methods [Sch06] and visualization (see Section 6.4.2), efficient data transfer via vertices is required.
We use such vertex-based communication schemes for a visualization of a water surface based on a DG shallow water simulation. Since DG discretizations are discontinuous at the cell boundary, a direct visualization of cell-wisely reconstructed water surface would lead to gaps in the surface. To overcome this non-intuitive visualization distracting the observer due to visible background color, we can construct a closed surface for visualization at each cell’s boundary, see Section 6.4.2 for details on the surface reconstruction.
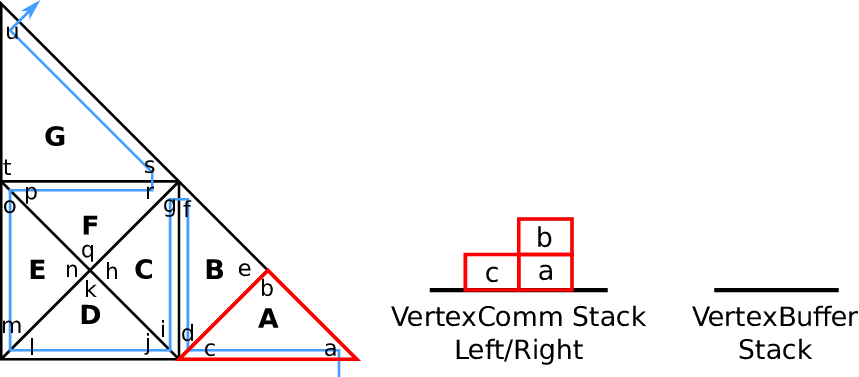
Edge communication with each edge shared by up to two cells requires storing of, receiving of and running computations on pairs of edge communication data only. For vertices, more than two cells typically share a vertex. Therefore, additional access policies are required:
Vertex touch policies:
During a grid traversal, vertices shared by other cells are either accessed the first, the last or between
the first and last time. We follow the terminology first-, middle- and last-touch [Nec09,Wei09]:
Instead of fetching an element from the stack, updating it and pushing it back, we only fetch the reference of this element and use the reference to update this data. This does not strictly follow the algorithmic and formal stack access pattern, but yields less operations and thus more performance.
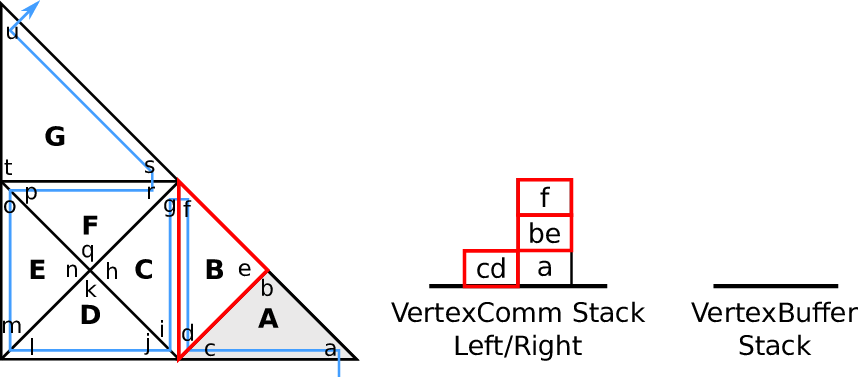
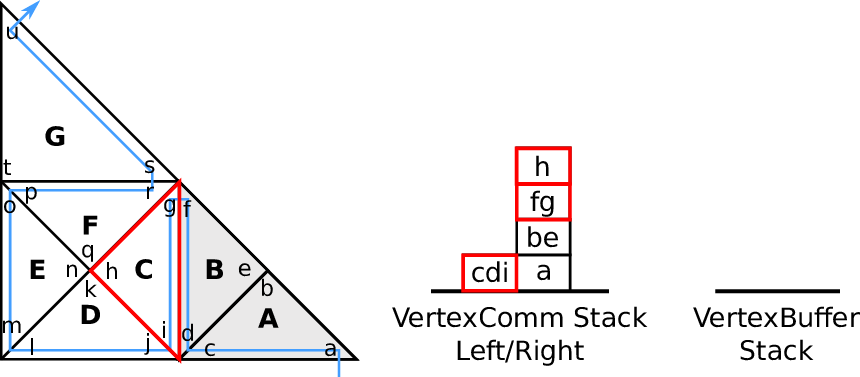
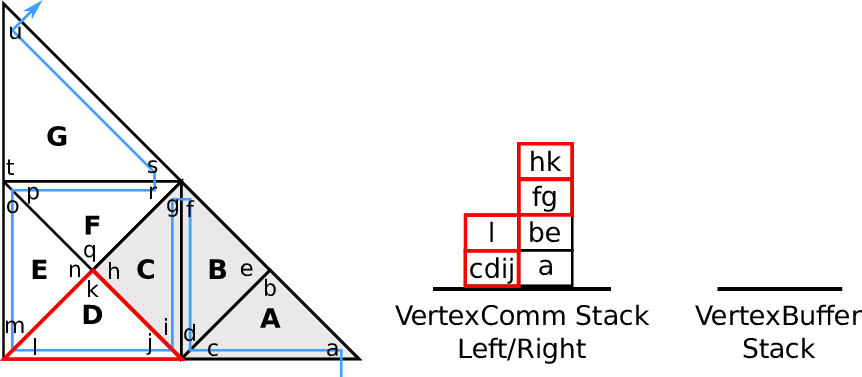
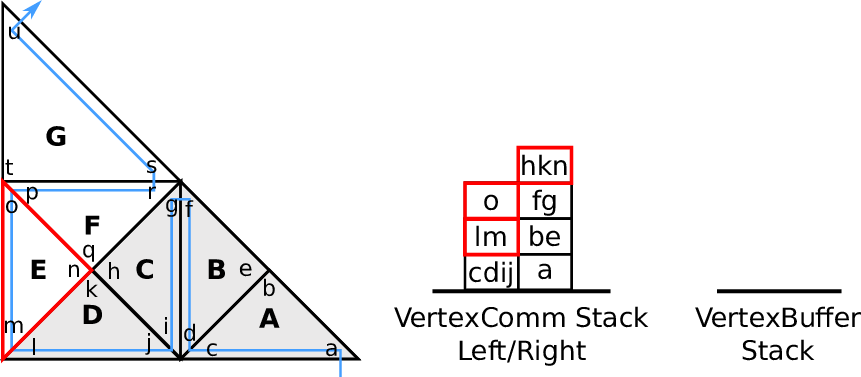
We just described different vertex access policies involved during grid traversal but still miss the knowledge which policy to apply. These policies are inferred based on the edge type labels only, with
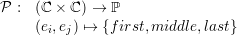 | (4.12) |
and both edges communication types (ei,ej) spatially touching the vertex as parameters. The vertex-access policy is then determined in the following way:
This also leads to the order of pair-wise edge communication types not being relevant for vertex access policy, yielding
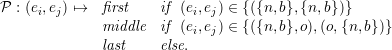 | (4.13) |
Finally, using the communication access order and edge types derived for each leaf element (see Section 4.3.2), the vertex-based communication for semi-persistent vertices via the stack system can be derived and applied with the information given above. An illustration is given in Fig. 4.6.
We like to emphasize, that we optimized the inference of the vertex access policies with a code generator, see Sec. 4.10.1. Hence, there are no if-branchings involved to distinguish between the different access policies presented above.
 |  |
 |  |
 |  |
 |