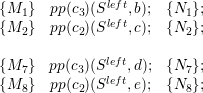4.7 Verification of stack-based edge communication

This section gives a formal proof of a valid edge-oriented communication between cells with the stack system using push and pop operations for the Sierpiński SFC. Using push operations on edges of type new and pop operations on edges of type old, the following theorem holds:

Proof:

The proof of the theorem is supported by axiomatic rules closely related to those of the Hoare calculus [Hoa69]. We define inference rules given in the form with A stating the condition which has to hold true and B the condition to replace A. The conditions are given by a tuple of tuples {{P}S{Q}}ⁿ with the precondition P, the code-statement S and the postcondition Q.

We further assume push and pop operations specified via push(S,a), pushing the element a to stack S, and pop(S,a) fetching element a from the stack.

The push and pop operations are extended with the pre- and postconditions

with the superscript k generating a unique labeling of the stacks.

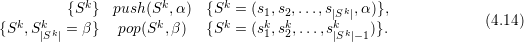
Reduction and commutative rules

Correct communication: The success of a correct pop operation by applying the grammar and inheritance of types lead to pop operations pop(S,α), testing for correct fetching of element α from the top of the stack. This leads to the rule

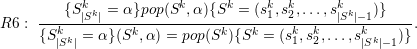(4.15)

This converts the pop operation into the pop operation introduced in Section 4.2, which allows reduction:

Reduction: Correct communication via push/pop to/from stack S^k is recognized and reduced via

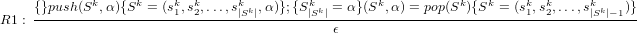(4.16)

This assures correct communication information received by the communication partner by pushing the same data α to the stack and fetching the same data α from the same stack. A reduction statement tests for such a correct communication and removes the statements, resulting in ϵ. We are allowed to do so, since the stack is kept in an unmodified state for all other edges accesses.

Commutativity: Commutative property for accessing different communication stacks

Those inference rules allow rearranging statements in case that they access different stacks. We emphasize here that this is only valid with constant data on each edge to be pushed to and fetched from stacks. This assumption would not be valid if e.g. data is fetched from one stack and data depending on this one pushed to another stack.

Joining consecutive communication data: In case of pushing or fetching edge data in the correct order with respect to the parent triangle allows to join data stored on the stack:

Here, α_r represents the edge data of the parent element. The edge data α_r on the hypotenuse of the parent’s cell can be split into two edges creating edge data α_r,1 and α_r,2. This rule has to be proven to assure correct refinement operations.

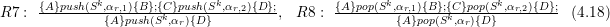
Application of inference rules

We apply the rules R1-R8 to show the valid stack access for edge-based communication. Considering only new and old communication types, the proof is given without loss of generality by boundary edges assumed to not modify any communication stacks. For even traversals, the access order for the root triangle only considering the edge access (see Section 4.3.2) is given by

Distinguishing between K, V and H traversals is not required (see Theorem 4.3.2). We associate the edge information (a,b,c) to the edges (e₁,e₂,e₃). Splitting a triangle using newest vertex bisection would then splits the communication information on the hypotenuse a by appending _,1 or _,2 to the subindex into (a_,1,a_,2). This would push two elements to the stack associated to e₁ in the correct order. We assume the inserted edge information to be equal to an arbitrarily choosen d.

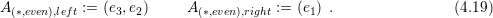
We map each new and old communication type of edge data α to push(S^k,α) and pop(S^k,α) to/from stack S^k. To avoid verification for all push/pop combinations, we use a generalization of stack operations

for the parent edges only.

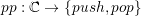
For the parent element of type even, this leads to the push and pop operations

It has to be proven that by applying the stack operations for both children, the stack modifications are equal to only applying the stack communication patterns of the parent element.

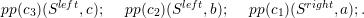
Our communication scheme with type inheritance

can then be applied resulting directly in the code for the stack operations being executed:

Using commutative rules (R2-R5), we can exchange the stack operations to

and by applying the reduction rule, this yields the half-diamond operations

Further applying our reduction rule R7/8 completes the first part of the proof since the reduction is only achieved in case of an exchange of data in correct order and correct order of push operations. This leads to

These stack operations on the data a, b and c are equal to the stack operations of the parent cell, assuming that this is the leaf cell. For odd element types, the verification is analogously given.

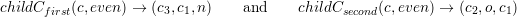
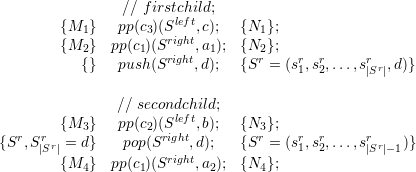
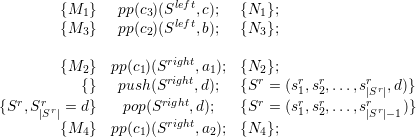
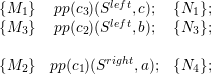
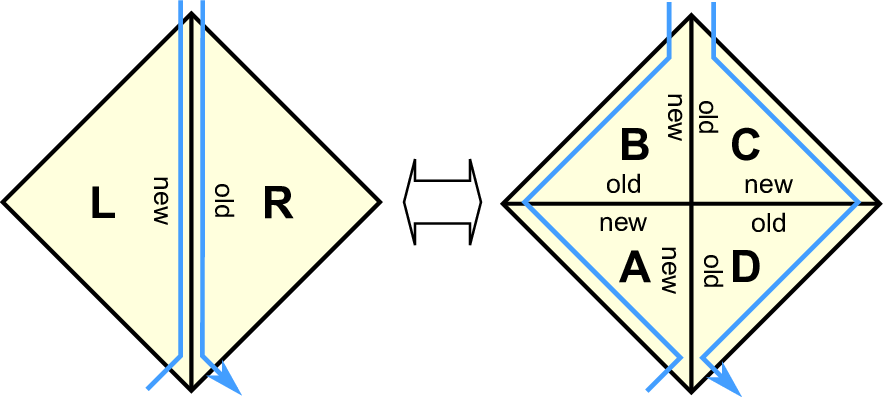
With our grids generated by the spacetree, we still have to prove the stack system for an entire grid. Without loss of generality, we only present this proof for diamond-shaped grid areas by applying coarsening rules, see Fig. 4.11.

---

Figure 4.11: Coarsening and refine operations with diamond shaped structure

---

We assemble two half-diamond operations (see Eqs. (4.20)) to operations of a full diamond and apply the coarsening operations. With operations on the right stack access represented by the symbol [X], this yields the following code

Applying the commutative and reduction rules, we can further reduce both push and pop operations to and with recursive induction, this results in a validated stack access. _

We just introduced a method for validating the correct communication via the left- and right stacks for two-dimensional triangular grids. Such a way of validation can play an important role on the search for valid stack-communication properties for other SFC-induced grids such as hexagons or higher-dimensional shapes.