These html pages are based on the
PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also
more information and a PDF version available.
4.8 Higher-order time stepping: Runge-Kutta
With DG simulations and their higher-order spatial discretization, the time-stepping method should
be of a similar (higher-)order. To determine the framework requirements, we selected the explicit
Runge-Kutta (RK) method. Considering the demands and algorithms shown in Section 2.14, RK
methods require storing conserved quantities at particular points in time to V i and their
corresponding derivative Di. Computing RK time step updates can then be achieved by additional
stacks SV 0 for V 0 and SDi for Di computed in each stage [BBSV10]. For an explicit RKn method
assuring accuracy up to n-th order with V 1 := V 0 due to ak,k = 0, we compute each stage i ∈{1,…,n}
with the following algorithm:
Algorithm: RK time stepping
Before iterating over the RK stages, the cell data SfsimCellData at the current time step is copied
to SV 0.
For i in (1,…,n) do:
-
(a)
- Compute Di := R(V i):
The simulation cell data stack SfsimCellData is assumed to be set to V i (see next step),
the conserved quantities computed within the current RK stage. The time step-typical
computations including edge communications are executed for SfsimCellData. However,
instead of updating the conserved quantities, only the change of the conserved quantities
over time is stored to SfsimCellData, yielding Di.
-
(b)
- Compute V i := V 0 + Δt∑
j=1nai,jDj:
After the grid traversal, Di is copied to SfDi. Then V i is computed and stored to
SfsimCellData by iterating over all elements of the stacks associated to V 0 and Dj and
applying equation (2.29).
Finally the time step is computed with
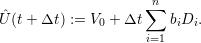 " class="math-display" />
" class="math-display" /> -
Since we use pointers to mark the beginning of the stack for both push and pop operations, it is
not necessary to copy stack data when assigning e.g. V 0 := U. Instead of copying the entire stack, we
can efficiently swap the stack pointers.
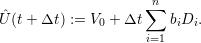 " class="math-display" />
" class="math-display" />