These html pages are based on the PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also more information and a PDF version available.

[next] [prev] [prev-tail] [tail] [up]

5.4 Base domain triangulation and initialization of meta information

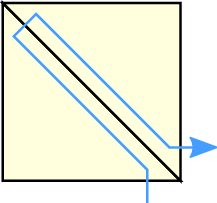
Simulations frequently demand being executed on domains with a different shape than a triangle or quadrilateral, e.g. a rectangular-shaped domain. The grid generation based on the Sierpiński SFC with the communication via stacks was so far accomplished only for a continuous SFC (see e.g.  [Vig12]) traversal of the grid. This leads to limitations of the shape of the simulation domain. Solutions which are also based on the linearized form of the leave nodes of a forrest of spacetrees (see [NCT09], this work is based on the Hilbert curve) introduced discontinuous SFC traverals. Such discontinuities in the SFC traversal allow spatial jumps on the simulation grid leading to an increased flexibility in domain configurations.

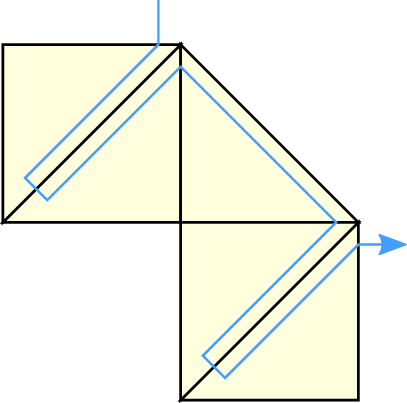
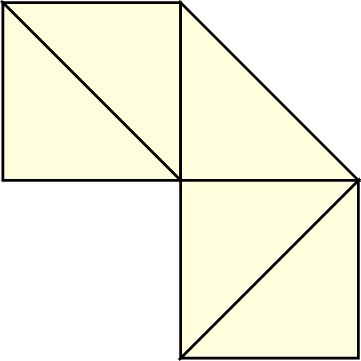
Since spacetree traversal is based on recursion, this makes such discontinuities challenging. Hence, we use an alternative domain assemblation: with our clustering based on subtrees, this allows domains of flexible shape being assembled by triangle primitives. This assemblation is considered to be valid, regarding our stack-based communication scheme, as long as all edges of the triangles are either not shared with other triangles or shared with exactly one triangle, see Figure 5.12 for examples. This requires setting up correct meta information in each cluster. Such information is e.g. run-length encoded communication information to/from adjacent clusters for communication with adjacent triangles and is further discussed in the next Section.

pict    pict pict    pict    pict

Figure 5.12: First two domains: examples for domain base triangulations with a traversal on a continuous Sierpiński SFC. Next three domains: Examples for domain base triangulations which cannot be represented by continuous 2D Sierpiński SFC traversal. The fourth domain is of particular interest for the cubed sphere grid, see Sec. 6.5.

5.4.1 Initial communication meta information

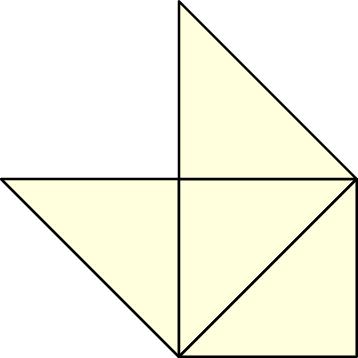
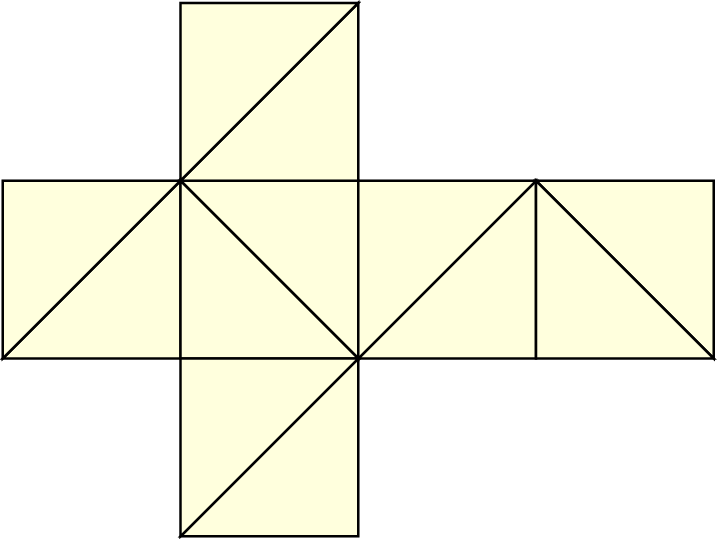
We initialize the inter-cluster communication based on clusters initially representing an entire spacetree. Each spacetree can also be based on a single leaf node. We refer to the spatial representation of these clusters as base triangles.

With such base triangles, the number of edge-communication elements on the left and right communication stack is given with

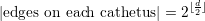
|edges on each cathetus| = 2⌊d2⌋
⌊d+1⌋ |edges on hypotenuse| = 2 2
with d the initial refinement depth.

For each base triangle, we determine the base triangles which are adjacent via all three triangle edges by searching for all possible adjacent base triangles via testing for shared edges vertices. This O(n) complexity for n clusters to search for base triangles sharing an edge can be assumed to be negligible for a small number of base triangles setting up the simulation domain.

The reconstruction of the vertex-based meta information requires further processing and is described in Sec. 5.5.4.

[next] [prev] [prev-tail] [front] [up]