With spacetrees [Fra00,Gün04,Pög04,Mun06,Nec09,Wei09], a particular domain Ω is initially represented in its non-refined state by a single cell. In a tree-like structure, this cell is represented by the root node of a tree. For refining a cell, two or more nodes are appended to the corresponding leaf tree node [Mit07], one node for each additional cell. Following this refinement scheme, the grid can be represented in a hierarchical tree with the leaf nodes representing the entire grid with non-overlapping cells. A serialization of the spacetree is then given by a depth-first traversal of the spacetree.
The spacetree used in this work is based on triangles and refinements of a cell based on the so-called newest vertex bisections [Mit07]. This bisection splits the triangle cell with the inserted refinement edge starting at the latest newest inserted vertex and the other vertex placed on the opposite edge. Such a bisection of triangles allows an adaptive mesh generation with an underlying binary tree with the Sierpiński SFC [HDJ04]. Bisecting an isosceles right-angled triangle, this refinement creates triangles of the same shape, only different in rotation, orientation and size. However, this does not limit the applicability to other triangle shapes: we can map triangle cells to a different shape and present this possibility for simulations on a sphere (Section 6.5).

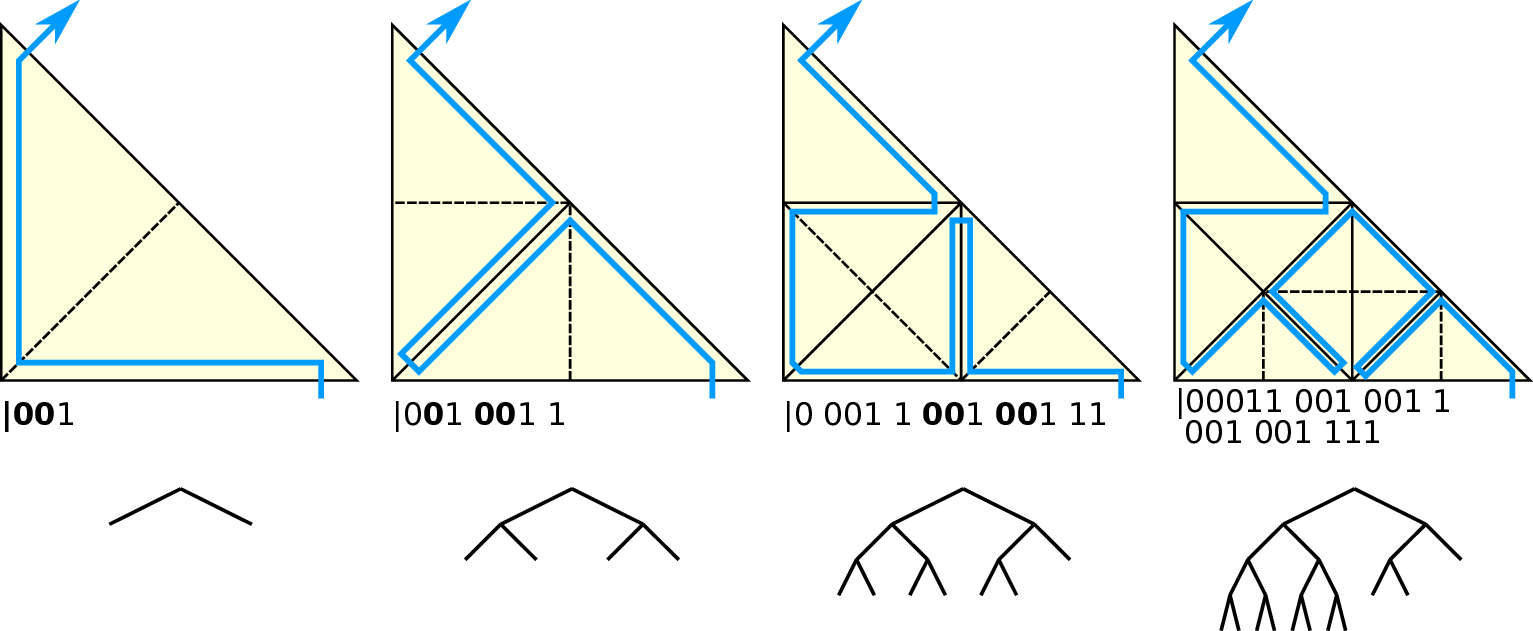
We can store the grid structure with a bit-stream (0 and 1) representing the spacetree structure. Traversing the grid can then be accomplished by successively reading elements of this structure stream and following the tree in a depth-first tree traversal in case of a 1 marker. In case of reading a 0 marker, we reached a leaf element which is a representative for a grid cell.
Refining a cell with newest vertex bisection can then be accomplished by replacing a single leaf-child bit 0 with 0,0,1 assuming that the bit stream is read from right to left. Coarsening of a cell is achieved by joining two cells which are children on the recursive tree traversal, thus replacing a sequence 0,0,1 with 0. Examples of different refinement states are given in Fig. 4.1. Note, that this can also lead to hanging nodes whereas we require a conforming grid (i.e. a grid without hanging nodes). The generation of a conforming grid with this property is further discussed in Section 4.6.