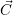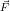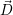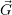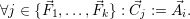These html pages are based on the
PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also
more information and a PDF version available.
8.3 Invasive resource manager
The content and structure of this section is related to our work [SRNB13b] which is currently under
review. A separate process runs in the background on one thread without pinning and executes the
resource manager (RM). The task of the resource manager is then the optimization of the resource
distribution and is based on the information provided by the applications via constraints. Such
constraints can be e.g. scalability graphs, workload and range constraints, see Sec. 8.2.1. For
sake of clarity, Table 8.1 gives an overview of the symbols used in this and the upcoming
section.
|
|
| Symbol | Description |
|
|
|
|
| R | Number of system-wide available computing resources |
|
|
| N | Number of concurrently running processes |
|
|
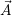 | List of running applications or MPI processes |
|
|
| ϵ | Placeholder for ”no application” |
|
|
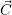 r r | State of resource assignments to applications |
|
|
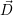 i i | Optimal resource distribution assigning Di cores to application Ai |
|
|
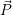 i i | Optimization information (scalability graphs, e.g.) for application
i |
|
|
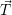 i i | Optimization targets (throughput, energy, etc.) for each
application |
|
|
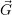 i i | Number of resources currently assigned to application i |
|
|
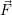 i i | List of free resources |
|
|
|
|
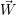 i i | Workload for application i |
|
|
| T(c) | Throughput for c cores |
|
|
| Si(c) | Scalability graph for application i. |
|
|
| |
Table 8.1: (source: [SRNB13b]) Overview of the symbols which are used in the data structures
of the resource manager.
Realization
The RM aims at optimizing the core-to-application assignment stored in the vector 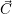 . Here, each
entry represents the association of the R = |
. Here, each
entry represents the association of the R = |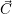 | physical cores to the applications. The application id is
stored to
| physical cores to the applications. The application id is
stored to 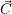 i if core i is assigned to the application. In case of no core assignment, ϵ is used as a
placeholder.
i if core i is assigned to the application. In case of no core assignment, ϵ is used as a
placeholder.
Scheduling information
Here, we describe our algorithm which optimizes the resource distribution based on the constraints
provided by the applications. Again, let R be the amount of system-wide available compute resources.
Further, let N be the amount of concurrently running applications, ϵ a marker for a resource not
assigned to any application and 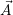 a list of identifiers of concurrently running applications, with
|
a list of identifiers of concurrently running applications, with
|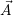 | = N. Then, we distinguish between management data inside the RM: uniquely per-application and
system-wide data.
| = N. Then, we distinguish between management data inside the RM: uniquely per-application and
system-wide data.
Per-application data: For each application 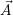 i, there is a
i, there is a 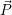 i storing the currently specified
constraints which were previously send to the RM via a (non-)blocking invade. The RM uses these
constraints for optimizations, depending on the desired optimization targets which are discussed in
Section 8.4.
i storing the currently specified
constraints which were previously send to the RM via a (non-)blocking invade. The RM uses these
constraints for optimizations, depending on the desired optimization targets which are discussed in
Section 8.4.
System-wide data: The system-wide management data is defined with the current resource
assignment 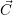 and an optimization target. Such optimization targets e.g. request a maximization of the
application throughput or for future applications the minimization of energy consumption.
Then,
and an optimization target. Such optimization targets e.g. request a maximization of the
application throughput or for future applications the minimization of energy consumption.
Then,
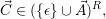 is
the current state on the resource assignment. This assigns each compute resource uniquely to either an
application a ∈
is
the current state on the resource assignment. This assigns each compute resource uniquely to either an
application a ∈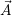 or to none ϵ. Then an optimization target is given e.g. by the optimal resource
distribution
or to none ϵ. Then an optimization target is given e.g. by the optimal resource
distribution
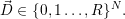 Here, each entry
Here, each entry 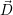 i stores the number of cores which are assigned to the i-th application
i stores the number of cores which are assigned to the i-th application
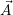 i.
i.
We further demand
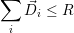 | (8.1) |
to avoid oversubscription of these resources. This avoids assignment of more resources than there are
available on the system. The resource collision itself is avoided by assigning the resources via the
vector 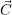 . Here, each core can be assigned to only a single application. Cores which are currently
assigned to an application are additionally stored in a list for releasing them without a search
operation on
. Here, each core can be assigned to only a single application. Cores which are currently
assigned to an application are additionally stored in a list for releasing them without a search
operation on 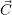 .
.
Optimization loop
A loop is used inside the RM which successively optimizes the resource distribution. Here, the resource
distribution is updated based on the constraints. Further, the current resource distribution 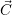 is
optimized towards the optimal target resource distribution
is
optimized towards the optimal target resource distribution 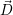 . The optimization loop can be separated
into three parts:
. The optimization loop can be separated
into three parts:
- Computing target resource distribution
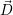 :
:
New parameters for computing the target distribution are made available to the RM via
constraints during setup, shutdown and invade messages. Here, the setup message yields
the constraint with a single core, whereas the shutdown message includes a constraint
which frees all cores.
The optimization function is executed every time if a new one is available (setup), a
constraint is updated (invade) or removed (shutdown). This optimization function is given
by
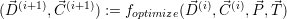 | (8.2) |
in its general form. Here, the vector of optimization targets is given in 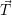 , e.g. targets such as
throughput or load distribution.
, e.g. targets such as
throughput or load distribution. 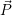 contains the application constraints and the current
distribution of cores to applications is given in
contains the application constraints and the current
distribution of cores to applications is given in 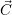 (i).
(i).
The computation of the target distribution with foptimize is further described in Section 8.4.
Then, 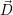 (i+1) contains the configuration of the computing cores to which the resource
distribution has to be updated and the superscript (i) annotates the i-th execution of the
optimization function.
(i+1) contains the configuration of the computing cores to which the resource
distribution has to be updated and the superscript (i) annotates the i-th execution of the
optimization function.
For applications which are sensitive to non-uniform memory access (NUMA), the target
core-to-application can be beneficial and is also returned in 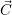 (i+1). In the current
implementation, this core-to-application assignment is not used and we continue using only the
quantitative optimization given in
(i+1). In the current
implementation, this core-to-application assignment is not used and we continue using only the
quantitative optimization given in 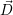 (i+1).
(i+1).
- Optimizing current resource distribution
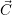 :
:
The RM successively updates the current resource distribution in 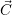 based on the theoretically
optimal resource distribution
based on the theoretically
optimal resource distribution 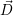 (i+1). A direct release of a core from an application is only
possible under special circumstances, e.g. if the core to be released is associated to the
application which is currently executing the (re)invade call. Otherwise, a message is
send to the application which has to release the core and the core may only be set
as free in the resource manager if the application sends a corresponding response
answer.
(i+1). A direct release of a core from an application is only
possible under special circumstances, e.g. if the core to be released is associated to the
application which is currently executing the (re)invade call. Otherwise, a message is
send to the application which has to release the core and the core may only be set
as free in the resource manager if the application sends a corresponding response
answer.
Given the list 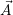 of applications, the resource redistribution is then optimized either by assigning
additional cores or releasing cores for each application. Here,
of applications, the resource redistribution is then optimized either by assigning
additional cores or releasing cores for each application. Here,
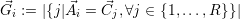 is the number of resources which are currently assigned to application
is the number of resources which are currently assigned to application 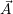 i. We then use
an iterative process over all applications
i. We then use
an iterative process over all applications 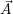 i to redistribute the resources over all
applications:
i to redistribute the resources over all
applications:
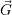 i =
i = 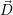 i: No update
i: No update
No further change in resources is required.
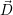 i <
i < 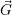 i: Release resources
i: Release resources
If less resources should be used by the application 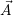 i, a message with this new
core constellations is send to the application. For non-blocking communication, the
message is send immediately to the application and for blocking invades, the resources
can be directly assumed to be released since the application directly updates the
number of used threads after waiting for the message of the RM. For non-blocking
simulations, the current resource distribution
i, a message with this new
core constellations is send to the application. For non-blocking communication, the
message is send immediately to the application and for blocking invades, the resources
can be directly assumed to be released since the application directly updates the
number of used threads after waiting for the message of the RM. For non-blocking
simulations, the current resource distribution 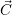 is not yet updated to avoid assigning
these resources to other applications.
is not yet updated to avoid assigning
these resources to other applications.
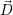 i >
i > 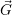 i: Add resources
i: Add resources
If additional resources should be assigned to the application, a search is executed in
the list of free resources 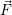 with
with 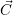
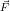 j = ϵ. Then, it assigns up to k ≤
j = ϵ. Then, it assigns up to k ≤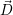 i-
i-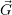 i resources
to the application with
i resources
to the application with
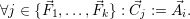
- Client-side resource update messages:
Every time the RM receives a resource update message from one of the applications, further
optimizations are executed since the change in resource utilization can lead to further
possibilities of resource optimizations. This executes the previously described iterative process of
resource optimizations.
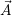
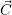 r
r 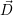 i
i 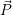 i
i 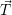 i
i 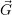 i
i 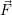 i
i 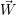 i
i 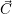 . Here, each
entry represents the association of the
. Here, each
entry represents the association of the 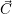
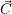
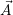 a
a 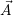
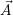
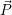
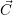 and an optimization target. Such optimization targets e.g. request a maximization of the
application throughput or for future applications the minimization of energy consumption.
Then,
and an optimization target. Such optimization targets e.g. request a maximization of the
application throughput or for future applications the minimization of energy consumption.
Then,
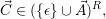
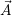 or to none
or to none 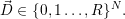
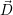
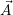
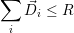
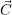 . Here, each core can be assigned to only a single application. Cores which are currently
assigned to an application are additionally stored in a list for releasing them without a search
operation on
. Here, each core can be assigned to only a single application. Cores which are currently
assigned to an application are additionally stored in a list for releasing them without a search
operation on 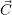 .
.
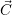 is
optimized towards the optimal
is
optimized towards the optimal 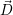 . The optimization loop can be separated
into three parts:
. The optimization loop can be separated
into three parts:
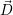
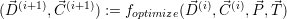
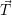 , e.g. targets such as
throughput or load distribution.
, e.g. targets such as
throughput or load distribution. 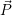 contains the application constraints and the current
distribution of cores to applications is given in
contains the application constraints and the current
distribution of cores to applications is given in 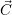
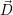
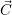
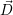
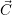
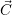 based on the theoretically
optimal resource distribution
based on the theoretically
optimal resource distribution 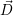
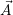 of applications, the
of applications, the 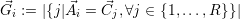
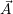
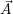
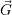
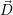
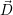
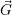
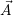
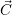 is not yet updated to avoid assigning
these resources to other applications.
is not yet updated to avoid assigning
these resources to other applications.
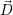
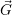
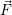 with
with