These html pages are based on the PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also more information and a PDF version available.

[next] [prev] [prev-tail] [tail] [up]

7.3 Invasive algorithms

With the knowledge about algorithms from the area of scientific computing, we developed numerical core algorithms in invadeX10. Such algorithms are a multigrid solver with changing workload due to restrictions and prolongations, a dynamic adaptive quadrature based on recursion and lightweight tasks and a Peano-SFC-based matrix-matrix multiplication [Bad08].

Since the multigrid solver with its multi-resolution access is one of the most interesting algorithms for invasion, we selected this solver to highlight the required changes in the program structure and like to refer to [TOS00] for a detailed introduction to such multigrid solvers.

pict  pict  pict

Figure 7.2: Heat distribution on a metal plate with a laser engraving symbols from left to right onto the metal [BRS+13].

As a representative application scenario, we selected a laser engraving symbols on a two-dimensional metal plate, see Fig. 7.2. This process can be simulated with the discretization of the heat equation which is discussed next, followed by a brief introduction to the multigrid algorithm which is then used to solve the system of equations.

Let the change in heat distribution over time for a two-dimensional problem be given by

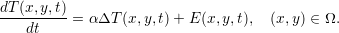
dT-(x,y,t) dt = α ΔT (x,y,t)+ E (x, y,t), (x,y) ∈ Ω.
on a domain Ω = [0,1]2 with the temperature T, the external energy E (e.g., a laser) and the thermal diffusivity coefficient α. We use Dirichlet boundary conditions of 0 on the domain boundaries dΩ. For the discretization in time, we use 1st-order forward differences and an implicit update scheme for the time stepping, yielding
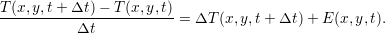
T (x, y,t+ Δt) - T(x,y,t) ------------------------ = ΔT (x,y,t+ Δt )+ E (x,y,t). Δt
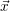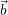This can be formulated with a system of linear equations A⃗x = ⃗b which can be solved with iterative solvers to compute an approximated solution.

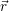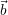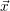Using a Jacobi solver, a single iteration mainly smooths the high-frequency errors, only. In case of low-frequency errors, multigrid solvers are commonly used. Here, we use the error-correction scheme of the multigrid solvers which restricts the residual ⃗r := ⃗ b- A⃗x* successively to coarser levels. Then, on each coarser level, we apply a Jacobi smoother iteration to compute the residual and restrict the residual to the coarser level. Each restriction operation then results in a reduction of the workload on each level by a factor of 4. After the execution of the smoother on the coarsest level2 , the computed error-correction is successively prolongated to the higher-resolved levels and an additional smoother iteration is executed before prolongating it to the next level.

With our heat equation and with a size of the simulation domain of 128 × 128, 7 levels with different resolutions are used. Since each level has a changing workload, this also results in a dynamical resource requirement.

For the parallelization, we use the distributed arrays from X10 to store the approximated solution ⃗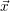x of the iteration, the right side ⃗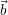b and the residual ⃗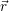r for each level.

Next, we compare a pseudo code of a non-invasive and an invasified multigrid algorithm in Fig. 7.1. To show the applicability of the dynamical resource management, we shrink the number of compute resources during the restriction.

Standard multigrid Invasive multigrid

vcycle(N, x, b): 
  r = computeResidual(N, x, b) 
  while |r| > threshold: 
    vcycleIteration(N, x, b) 
    r = computeResidual(N, x, b) 
 
vcycleIteration(N, x, b): 
  smoother(N, x, b)       # Pre-smooth 
  r = residual(N, x, b)   # Residual 
 
 
  Nr = N/2                # Restricted Level 
  rr = restrict(N, r)     # Restrict Residual 
                          # To new Claim 
  er = floatArray(Nr, 0)  # Setup with 0 
  vcycleIteration(Nr, er, rr)  # V-Cycle 
 
 
 
 
 
 
 
  e = prolongate(Nr, er)  # Prolongate error 
  x = x + e               # Apply correction 
 
  smoother(N, x, b)       # Post-smooth 
  return

vcycle(N, x, b, homeClaim): 
  r = computeResidual(N, x, b, homeClaim) 
  while |r| > threshold: 
    vcycleIteration(N, x, b, homeClaim) 
    r = computeResidual(N, x, b, homeClaim) 
 
vcycleIteration(N, x, b, claim): 
  smoother(N, x, b, claim)       # Pre-smooth 
  r = residual(N, x, b, claim)   # Residual 
  nc = reinvade(Nr, claim) # Reinvade Claim 
 
  Nr = N/2                # Restricted Level 
  rr = restrict(N, r, nc) # Restrict Residual 
                          # to new Claim 
  er = floatArray(Nr, 0, nc)  # Setup with 0 
  nc2 = vcycleIteration(Nr, er, rr, nc)  # vcycle 
 
  # Redistribute due to changed Claim 
  if (nc != nc2): 
    nc = nc2                 # Update Claim 
    x.redistribute(Nr, nc) # Data Migration 
    b.redistribute(Nr, nc) # Data Migration 
 
  e = prolongate(Nr, er, nc) # Prolongate Error 
  x = x + e                  # Apply Correction 
 
  smoother(N, x, b, nc)      # Post-Smooth 
  return nc  # Return possibly modified claim


Table 7.1: Comparison of pseudo code for non-invasive and invasive versions of the X10 multigrid [BRS+13].

Based on the invadeX10 framework, each v-cycle iteration is extended with the claim as a parameter which describes the currently invaded processing elements. The resources in these claims can be dynamically changed with a reinvade, based on the number of slices of the solution array on the currently restricted multigrid level. In case that a reinvade led to a change of resources (nc != nc2), also the distributed arrays are redistributed to improve the locality to the computing resources.

[next] [prev] [prev-tail] [front] [up]