6.6 Multi-layer simulations

With the shallow water equations, a simplification of an originally three-dimensional model is used. This allows computationally more efficient simulations with results close to the three-dimensional formulation. This is not possible in all cases such as weather and climate simulations. Considering e.g. the model used by the Deutscher Wetter Dienst (DWD), a multi-layer discretization in the vertical direction is used to simulate three-dimensional effects.

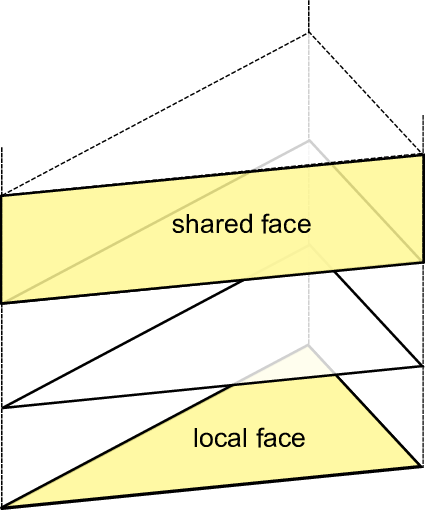
We also extended our framework with such a multi-layer approach. Here, we present the multi-layer simulation of the Euler equation. A constant number of layers is assumed in each grid cell. The two-dimensional cell-data storage is then used to store a pile of three-dimensional cells. We introduce a new terminology for this extension: the three-dimensional cells are further denoted as volumes. Edges are further described as adjacent faces and the shared interfaces of two piled cells are named local face, see Fig. 6.13.

For a basic 3D DG simulation, the following major building blocks of a multi-layer simulation are required:

1.

Gather flux parameters on faces.

2.

Compute fluxes on adjacent faces and local faces.

3.

Compute time step size.

4.

Based on flux updates and time step size, integrate the time in each volume.

We also have to compute the time step size for the local faces. This would require an extension of the framework with additional interfaces. However, we overcome this by utilization of (a) the cluster-local user data to temporarily store flux updates and (b) the kernel interfaces for storing edge communication data:

• Executing flux computations for local faces:
  For communication of flux parameters via edges, the corresponding interface is executed exactly once for each triangle edge and for each time step.

  Hence, we can use one kernel handler, e.g. for the hypotenuse (cell_to_hyp). This allows us to compute fluxes for the local faces.

• Storing flux updates:
  After computing the fluxes for the local faces, these fluxes have to be temporarily stored until the time step size is known. Since we aim at memory efficiency computations, we do not store the fluxes in each cell, since they are e.g. not required during adaptivity, but we extend the cluster-local user data with an additional stack system to temporarily push computed fluxes to this stack.
• Computing time step size:
  We also store the wave speed computed for the local faces to cluster-local user-data. After computation of the fluxes with the adjacent faces of the cluster, the wave speed from the local faces is involved in returning the per-cluster maximum wave speed required for computing the maximum time step size.
• Time stepping:
  With the flux updates for the adjacent faces and for the local faces fetched from the cluster-local stack, the DoF are advanced in time.

This extension finally leads to the capability of handling multi-layered simulations transparently to the framework which was originally only developed for two-dimensional simulations.