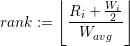
Our distributed-memory parallelization approach takes advantage of our cluster-based software design with a replicated data scheme also for shared-memory parallelization. This also accounts for the two major issues for distributed memory systems: (a) efficient block-wise communication via RLE meta information and (b) efficient data migration with the cluster-based software design. Furthermore, our software design makes the extensions for distributed memory almost transparent for a framework user since only minor additional requirements for the framework user are induced such as the data migration of user-specified data.
Support for distributed memory can then be accomplished with the following extensions to the framework design (Fig. 5.10):
Considering the components relevant from an algorithmic point of view, the distributed memory parallelization is then based on items (2)–(5) which are further discussed in detail.
Regarding the cell communication, requirements on (a) intra- and (b) inter-cluster communication are discussed next:
Regarding the inter-cluster data exchange, we use non-blocking send operations to transfer the replicated data to the rank of the adjacent cluster. Using our RLE, this data transfer can be obviously accomplished directly block-wise, e.g. without gathering of smaller chunks of data to be transferred.
We further use MPI send-recv tags to label each communication with the communication data being either stored to the communication buffers in clockwise or counter-clockwise order of the SFC close to the inter-cluster shared hyperfaces. This is required for base triangulations consisting e.g. only of two triangles with periodic boundary conditions. This avoids the communicated data stored for clockwise edge directions being read for edges with counter-clockwise direction and vice versa.
Depending on the method of data exchange on distributed-memory systems, our approach can further demand for a particular order and tagging. To receive the data blocks in correct order, the send operations follow the SFC order of the clusters and the receive operations are then executed in reversed SFC order. Also the RLE meta information entries have to be iterated in reversed order to consider the opposite direction of the traversal of the clusters at the other rank (see Section 5.2.5 for information on reversing communicated data). Reversing these receive operations assures the correct order.
For load-balancing reasons, it can be advantageous to split a cluster in case that its one-dimensional SFC interval representation can be assigned to several cores.
The cluster generation approach considered in this work is based on the rank-local number of cells only. This makes the cluster generation approach independent of the global load distribution. An extension with a global parallel prefix sum based on the number of cells [HKR+12] to generate cluster in a global-aware manner is not further considered in this work.
After splitting and joining of clusters, we also require reconstruction of the communication meta information to account for possible splits and joins of adjacent clusters. Updating local RLE meta information that is associated to a cluster stored at another rank is not possible anymore with our shared-memory approach, see Sec. 5.5.3. This is due to a missing direct access to the meta information of the adjacent cluster. Therefore, the adjacent cluster is responsible for deriving and sending the required split/join information. The local cluster then receives and uses this information to update the RLE meta information accounting for adjacent split/join operations.
With dynamically adaptive grids, this results in load imbalances across several ranks. Data migration is one of the typical approaches to migrate workload to another rank. With our cluster-based data migration, we present a highly efficient method for migrating a set of clusters. This efficiency results from three major components of our software design:
The migration algorithm of our cluster then consists of the following steps:
For efficiency reasons, we joined this step with updating the RLE information during forwarding the information for dynamic clustering (Section 5.10.2).
After receiving all clusters at a rank, the pointers to the adjacent clusters which are stored on the same rank have to be recovered, e.g. for accessing meta communication data. By also keeping the cluster-unique id in each RLE meta information entry, we can find the clusters efficiently with the cluster set based on a binary tree structure. The pointers from the adjacent cluster to the currently processed one can then be directly corrected by writing to the RLE meta information of the adjacent cluster.
We emphasize that these writing operations to adjacent clusters violate our push and pull concept (no writing access to adjacent clusters). However, we consider this to be the most efficient way to update the communication meta information for clusters stored on the same memory context.
For clusters migrated away from the considered rank, the RLE meta information of the adjacent clusters on the same considered rank have to be updated. These entires are set to the new rank to which the cluster was migrated to. This new rank is available with the destination rank label, see the first item (1) of this list.
The information where to send the clusters is derived based on the local and MPI parallel prefix sum on the number of cells in each cluster. Then, each rank can determine the current range of cells within the global number of cells of the entire simulation. The clusters are tagged with a rank which leads to improved load balancing. Such a load balancing can be e.g. improved by sending the clusters only to the next or previous rank. This is advantageous, since only the next and previous rank have to test for a cluster migration from an adjacent node. For severe load-imbalances, such a migration is not feasible anymore since only an iterative data migration can solve such a load imbalance. Hence, we can tag the cluster to be directly sent to the rank which should own the cluster for improved load balancing. Here, the rank is computed by
Since our cluster migration is based on setting the destination rank followed by the cluster migration, this allows implementing a generic load-balancing interface [DHB+00] and, thus, also different well-studied load-balancing and migration strategies, see e.g. [ZK05,Cyb89,Hor93].

With our communication scheme relying on the correct SFC order of the underlying grid cells, we are not allowed anymore to generate domain triangulations such as the one given in Fig. 5.35. In general, traversals with an initial base triangulation and an SFC traversal close to shared edges in the same direction (see e.g. [NCT09] for a cubed sphere SFC traversal with the Hilbert SFC) result in inconsistent communication schemes.
A different view of a correct communication order for base triangulations on distributed-memory systems is the possibility of embedding our grid into a (regularly) recursively structured grid based on the Sierpiński SFC. This consequently leads to the space-forrest assembled by the nodes on a particular level of a regularly refined spacetree. Examples for invalid and valid base triangulations with the corresponding embedding into a regular refinement are given in Fig. 5.36.
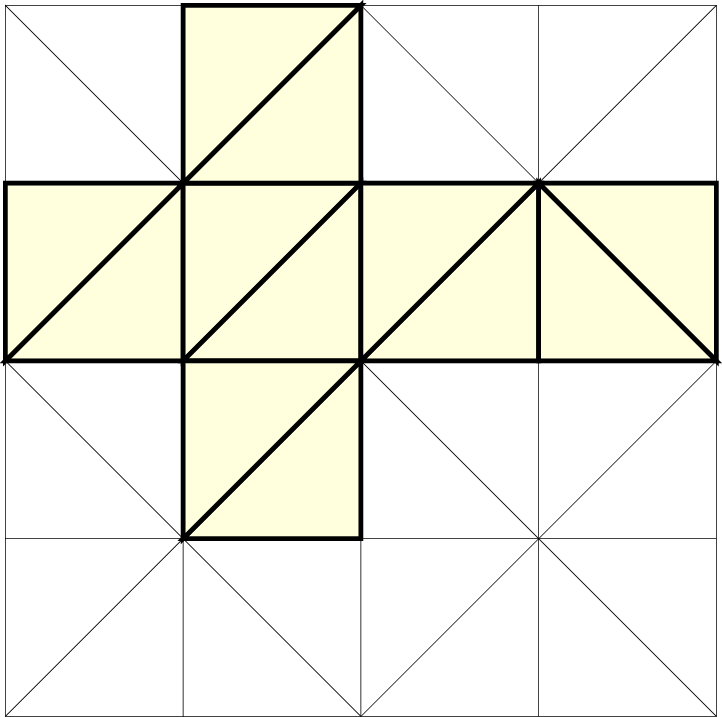
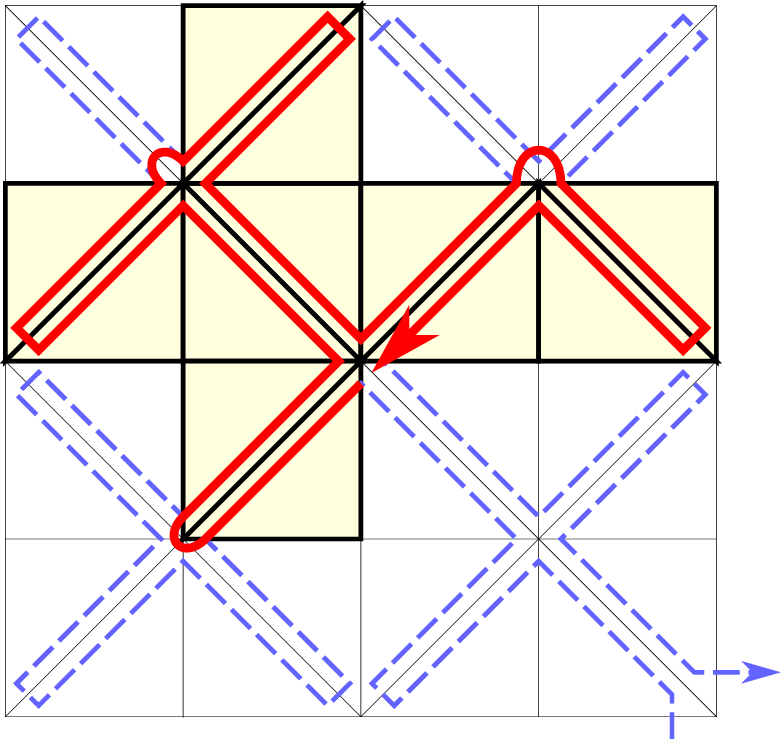
The initial association of base triangles to ranks is accomplished by aiming for balanced workloads. Embedding our base triangles into an SFC generated grid, we can again use the 1D representation to assign clusters to ranks. Each rank then initializes the clusters assigned to it. Regarding the cluster tree, each rank removes all leaf nodes not assigned to the current rank and also the inner nodes which do not have any further child nodes.
We continue by highlighting similarities between clustering and dynamically adaptive block-adaptive grids.
Hence, a cluster-based parallelization approach allows similar optimizations such as hybrid parallelizations, latency hiding, etc. with some of them being also further researched in this work.