Inter-partition communication and dynamic meta information

These html pages are based on the PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also more information and a PDF version available.

[next] [prev] [prev-tail] [tail] [up]

5.2 Inter-partition communication and dynamic meta information

With partitions generated by the SFC intervals, we present communication patterns by generating and synchronizing data shared interfaces of partitions with a replicated data scheme. First of all, a replicated data scheme requires independent communication buffers. To account for these replicated data scheme, we use additional stack-based communication buffers for each partition. We continue with a static number of partitions and refer to Section 5.5 for dynamic partition generation.

5.2.1 Grid traversals with replicated data layout

For our Sierpiński stack- and stream-based traversals, we first describe the replicated data layout in an abstract way. It can be implemented with a forward- and backward-traversal in the following way:

(a): Forward traversal:
During the forward grid traversal of partition P_i, the edge types of all shared interfaces on the partition are set to new. With our grid traversal based on recursion and inherited edge types, the edge types for the shared interfaces can be directly set to new and old at the sub-tree’s root node.
By executing an SFC-based grid traversal, communication data is written to the corresponding edge- or vertex-communication stacks. Since those output buffers are replicated, this access is race condition free. Now, the output stacks are filled with communication data of dP_i.
(b): Synchronization:
Working on replicated data, we execute a reduce operation for the data stored at shared interfaces to synchronize the replicated data on the communication buffers. Information on the placement of shared interface data dP_i in memory buffers is provided in Section 5.2.3.
(c): Backward traversal:
Finally, a backward SFC traversal is reading the data from communication stacks by setting the edge types of shared interfaces to old. This results in reading the communication data on which the reduce operation was executed on.

A parallelization with a replicated data scheme allows the forward traversals being executed on all partitions in parallel and also in arbitrary order. The same holds for the synchronization operation and backward traversals. Therefore, the only required access-synchronizations are between the forward, reduce and backward traversals. So far, this is a similar approach which was also taken in [Vig12].

5.2.2 Properties of SFC-based inter-partition communication

We next discuss important properties by using the Sierpiński SFC with a stack- and stream-based communication.

Lemma: 5.2.1 (Order of replicated data) After the first traversal, the elements on the communication stack are ordered with their creating SFC cell indices.

Proof:: This theorem directly follows from Theorem 4.7.2 on page 166 due to correct order of the elements on the communication stacks also during the grid traversal. _

With communication data ordered with the SFC cell indices, this also leads to additional and for our development mandatory properties regarding the cardinality and uniqueness of data exchange:

Theorem 5.2.2 (Unique adjacent partition) All communication data for an adjacent partition P_k are consecutively stored on the communication stack. This induces an unique adjacency of partitions.

Proof:: The proof is given by reductio ad absurdum with the communication element order from Lemma 5.2.1. Let at least two consecutively stored non-empty communication data sets S₁ and S₃ on the communication stack shared with an adjacent partition P_a and a set S₂ associated to P_b be given. S₁, S₂ and S₃ are consecutively stored on the communication stack. Further, let the communication data consist out of SFC-ordered cell indices. Then, there has to be at least one partition P_b with a≠b accessing the elements stored between the communication elements which are stored for partition P_a on the communication stack. However, this leads to a contradiction to Lemma 5.2.1, page 207: with all cell indices from P_a within a particular SFC interval, the cell indices from P_b then have to be within the range of P_a. With our grid partitioning approach (see Section 5.1.1), this is not possible due to consecutive intervals (without gaps) assigned exclusively to each partition. _

5.2.3 Meta information for communication

So far, we assume the knowledge on which blocks of data stored on the communication stacks are associated to which partition to be already given. We refer to this knowledge as communication meta information.

We can store this information per partition and not per cell due to two properties given by the SFC stack-based communication:

1.: The adjacency information per cell is not required for inner-partition hyperfaces due to stack-based communication.
2.: We can store and manage data on shared interfaces _i,j efficiently with a run-length encoding per partition which we present next:

Run-length encoded adjacency information:

We continue with a description of the meta information for communication and how it is managed. Searching for adjacency data for each communication element can be time-consuming if iterating over all adjacency information stored for all shared hyperfaces or stored per cell. For node-based communication with each node adjacent to up to 8 cells, managing adjacency information can be also very memory demanding.

We present a solution based on both previously derived theorems:

Lemma 5.2.1 provides the property of all shared interfaces particularly ordered on the stack system with respect to the SFC-based index of the cell generating the data. Using this property, we can access the data at the adjacent partition en bloc without considering per-hyperface meta information. This is due to the same quantity of data also being stored ordered and en bloc on the communication buffer of the other partition. Using the order of both replicated chunks of communication data, the corresponding replicated data placement for each hyperface can be induced.
Theorem 5.2.2 assures that each consecutive chunk of data is stored only once per adjacent partition. For partition P_i, let the consecutive set of shared interfaces I_i,k be given preceeded and followed by shared interfaces associated to other partitions. Then, there is no other set of shared interfaces which is associated to partition P_k. For partitions generated by spacetree splits, we can also use the geometric convexity of the subtree to assure the uniqueness of a set of shared interfaces associated to an adjacent partition.

[ERRATA / COMMENT: We developed this proof to assure that the RLE connectivity information for our clustering approach (developed in 2011) works properly in all cases for data exchange, for updating the RLE connectivity information via edge-split/merge adaptivity markers, to infer the new connectivity information during the cluster generation, etc. and finally to proof that the possible extension to SFC cuts really works (see http://www5.in.tum.de/~schreibm/private/thuburn/extracted/dynamic_adaptive_grids/2012_06_13_lst_treffen.pdf). In the context of solely focusing on optimizing communication for MPI send/recv, a similar proof can be also found in "Space-filling curves", Michael Bader, Sec. 10.6.2. ]

This allows introduction of a run-length-encoded (RLE) representation of the adjacency information.

pict

Figure 5.4: Example for an RLE edge communication meta information. The domain is partitioned via subtrees of the spacetree into partitions A-F. Here, we discuss the RLE edge meta communication information for partition B. Regarding the left edge communication stack, three edge communication data elements (a,b,c) are stored to the left edge communication stack after the first forward traversal. These shared edges are adjacent to partition A and encoded with the RLE (A,3). For the right communication stack and following the SFC induced edge access with the forward traversal in partition B, the first adjacent partition is E via two edges, hence using the RLE entry (E,2). This is followed by partition C with only one edge which is encoded with RLE entry (C,1).

pict

Figure 5.5: An example of a sparse communication graph representing our RLE meta information for edges. Each graph edge represents one entry in the RLE meta information.

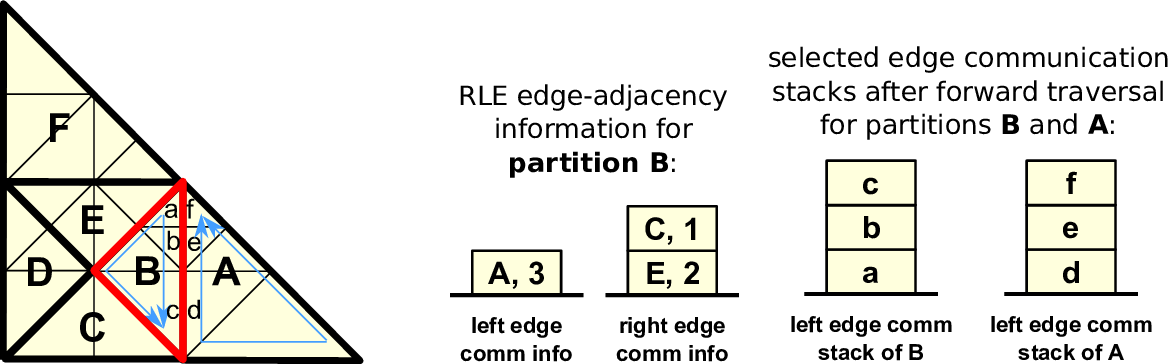
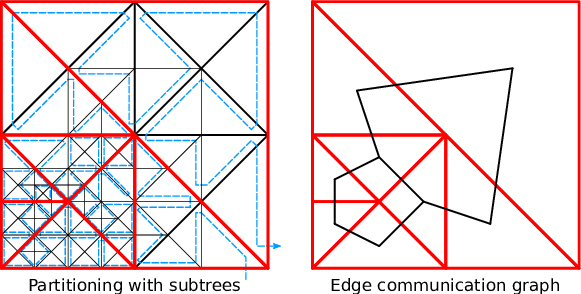
We first consider one-dimensional shared interfaces (edges) only and the information on communication edges for adjacent partitions A, B and C, respectively, given by 2, 4 and 3 shared edges. Without RLE, we can store the meta information with the tuple (A,A,B,B,B,B,C,C,C). Using our RLE, we represent m entries for edge communication referring to the same adjacent partition P with the tuple R := (P,m). We can compresses this with an RLE scheme to ((A,2),(B,4),(C,3)). Figure 5.4 gives an example of such an RLE edge communication for a single partition and Figure 5.5 shows the underlying representation of the sparse edge communication graph.

For the zero-dimensional hyperfaces (nodes), we can extend the RLE representations for the edges directly accounting for nodes: We first require that no zero-length encoded communication information for edges may be stored. This allows us to use RLE elements with m = 0 to describe a vertex shared with an adjacent partition which was not considered by the edge-based communication so far.

pict

Figure 5.6: Sparse communication graph for edges and nodes. Left image: grid representation. Right image: communication graph for the given underlying grid. Solid line graph edges represent communication for edges whereas a dashed graph represents communication for nodes of partitions not represented by RLE for edge communication meta information.

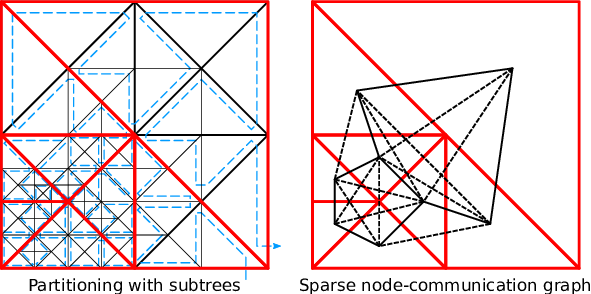
To give an example, we assume adjacent partitions A, B and C, sharing hyperfaces setup with 2 edges, 1 vertex and 3 shared edges, respectively. Storing the information on edges and vertices separately would result in edge encodings (A,A,C,C,C) for the edge communication information and (A,A,A,B,C,C,C,C) for the vertex communication information. Unifying both representations with tuples and additional markers e and v representing edges and vertices yields ((A,e),(A,e),(B,v),(C,e),(C,e),(C,e)). Here, we assume that two consecutive and identical entries also account for a vertex. Using our RLE scheme, this meta information can be further compressed to ((A,2),(B,0),(C,3)). The underlying sparse communication graph is given in Fig. 5.6. This RLE meta information is stored separately for the left and right communication buffers.

We summarize the main benetifs of using such an RLE compared to meta information stored for each shared hyperface:

(a): Less memory is required to store adjacency information.
(b): We can use block-wise communication for shared- and distributed-memory communication.
(c): We can implement an efficient implicit management of RLE meta information for our adaptivity traversals (see e.g. Section 5.2.6).

By considering the communication of cell ids, the SFC traversal at the adjacent partition generates the data on the communication stacks in reversed, descending, order. This leads to the requirement of reversing the order of elements transferred block-wise.

5.2.4 Vertices uniqueness problem

So far, we ignored the vertices at the cell touched at first and last during traversal of a partition. The data associated to this vertex can be stored to either the left or right communication stacks. We consider two solutions for this uniqueness problem:

SFC traversal aware:
The algorithm for determining the position of the communication data considers whether the vertices have been stored to the left or right communication stack. This can be done by taking the SFC traversal for the first and last entered cell into account.
SFC traversal modification:
An alternative approach is to modify the SFC traversal and, thus, forcing the first and last node to be either stored to the left or right stack.

We decided to use the modification of the SFC traversal for the present work: with our recursive subtree traversal, we override the underlying SFC traversal grammar G on the subtree’s root node to force the placement of the first and last vertex to the left or right communication stack. Then, we use this uniqueness to derive the knowledge on the placement of the vertices on the communication stacks.

5.2.5 Exchanging communication data and additional stacks

So far, we know the amount of data and from which adjacent partition to read the data from. With our parallelization based on the replicated data scheme (see Sec. 5.1.2), we use separated buffers for the inter-partition shared hyperfaces. However, exchanging data with adjacent partitions using the same stacks for receiving data as for writing data leads to race conditions. Therefore we extend the stack system with buffers storing the exchanged or, in combination with the communication buffer, the reduced data in case of a reduce operation. This additional exchange stack is then used by the backward traversal instead of the communication stack during the forward traversal. Such additional exchange stack requirements lead to a duplication of each communication stack due to our replicated data scheme.

We further differentiate between shared- and distributed-memory data exchange:

For shared-memory systems, an access to communication data can be directly achieved by additionally storing a pointer to the adjacent partition in each RLE information. This allows accessing the adjacent partition directly and looking up the position of the replicated interface data on the adjacent communication stack efficiently with the RLE meta information, see Sec. 5.2.3.
For distributed-memory implementations, we extend the RLE entry with a rank and set this to the rank which owns the adjacent partition. We can then distinguish between partitions stored on the same rank or on another rank by either comparing the rank in the RLE entry with the local rank id or by introducing a special rank, e.g. -1 to represent partitions in the same memory context.
In case that partitions are existing in the same memory context, the data exchange method is identical to the shared-memory implementation.
If both partitions are stored on different MPI ranks, we send the local replicated data block-wise by using our RLE meta information. Hwere, we lookup the memory location on the communication stack and the rank information for the destination of the message, followed by a non-blocking send. The receive operation is analogous to the send operation, but uses the exchange communication stack as the receive buffer. Further information is available in Section 5.10.

5.2.6 Dynamic updating of run-length-encoded adjacency information

The communication to/from cells adjacent via hyperfaces can be accomplished with our communication stack system and the RLE adjacency information. Due to our dynamically adaptive grids, this adjacency information has to be updated appropriately for dynamically changing grids. To avoid a reconstruction of the meta information, e.g. based on the recursive spacetree traversal, we use additional information stored on the communication stack during our last adaptivity traversal.

Instead of running only the last backward adaptivity traversal to refine and coarsen cells, we also transfer additional information on inserted and removed edges via the edge communication stacks. To generate data for the partition boundary dP_i, we set the edge types of the partition boundaries to new and forward the following markers via edges:

Refine marker M_R:
The marker M_R is pushed to the edge communication stack for edge e_i in case that a refine operation demands inserting an edge creating a vertex at edge e_i.
Coarsening marker M_C:
For a coarsen operation, the marker M_C is written to both edges associated to the triangle legs. This accounts for this edge being involved into a coarsening operation. We consider two cases: (a) the edge is shared between the two cells which are joined with the coarsening. Then, this edge is removed and also the forwarded coarsening marker M_C is fetched from the stack system. (b) the edge is not shared between the two cells which are joined with the coarsening. Then, this edge is not joined with the edge of the other cell involved in the coarsening process. Hence, the marker M_C is written twice to the communication stack.
No operation M₀:
In case that neither the marker M_R, nor the markers M_C was transferred via the edge, the marker M₀ is pushed to the edge communication system. This accounts for an edge not being modified due to adaptivity.

After the grid traversal, the left and right edge communication stacks then store adaptivity markers on split (M_R: inserting a vertex) and joined (2 × M_C: removing a vertex) edges for the partition boundary dP_i. This allows us to update the RLE meta information of the modified grid based on these markers only. An example is given in Fig. 5.7.

Updating the left and right RLE meta information is then accomplished by iterating over the respective adaptivity communication stack to which the adaptivity markers were written to. These markers describe the change in the RLE meta information due to the adaptivity step.

Algorithm: Updating communication meta information

For markers M_R, the RLE information associated to the adjacent partition has to be incremented by 1 due to an additional edge inserted.
The marker M_C is handled in a different way: due to the diamond coarsening shape (Fig. 4.10), only pairs of M_C are allowed. The corresponding RLE is then decremented by 1 for each pair of coarsening markers M_C stored on the communication stack.

pict

Figure 5.7: Updating meta information for the communication being based on adaptivity refinement (M_R = R) and coarsening markers (M_C = C). Note that the adaptivity markers are stored in backward traversal direction. For a single refinement marker R, the corresponding RLE entry has to incremented by 1 to account for the inserted edge. Reading two coarsening markers C from the adaptivity communication stack, this is a representative for a removed single edge. Therefore the RLE entry is decremented by 1 [SBB12].

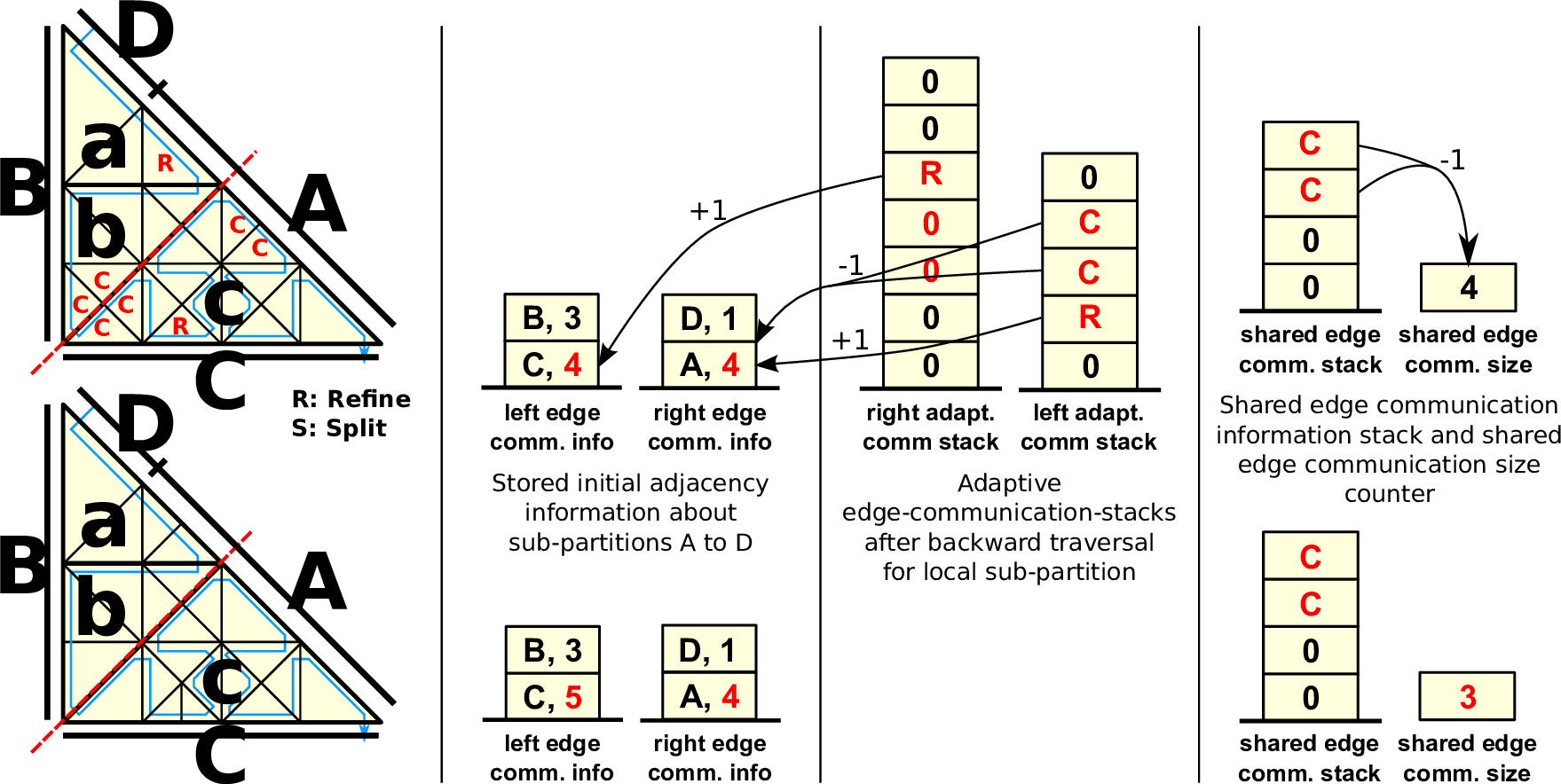
Updating the vertex communication data is also transparent to this adaptivity process. By adding or removing edges via updating the RLE, this also accounts for updating the vertex-based communication information due to three properties:

Adding an edge by increasing the RLE also considers the additional vertex.
Removing an edge by decreasing the RLE also considers the removed vertex.
Explicitly stored vertices with RLE of 0 are transparent to edge insertions since all refinement states do not modify 0-length encoded vertex information.

Special care has to be taken for partitions consisting only of a single cell since a coarsening operation would lead to a partition only consisting of half a cell. These coarsening operations must be deactivated by invalidating the coarsening state on the adaptivity state stack.

The presented communication schemes are also applicable to partitions generated by SFC cuts.

[next] [prev] [prev-tail] [front] [up]