SFC-based parallelization methods for DAMR

These html pages are based on the PhD thesis "Cluster-Based Parallelization of Simulations on Dynamically Adaptive Grids and Dynamic Resource Management" by Martin Schreiber.
There is also more information and a PDF version available.

[next] [tail] [up]

5.1 SFC-based parallelization methods for DAMR

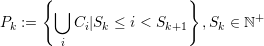
Parallelization of simulations with (dynamic) adaptive mesh refinement has a rich history in scientific computing. SFC-based domain decomposition and load-balancing strategies are considered to be among the most efficient regarding our requirements of a changing grid in each time step (see related work in Section 3.4.1), and we continue with a more detailed introduction to SFC-based domain decomposition methods.

5.1.1 SFC-based domain partitioning

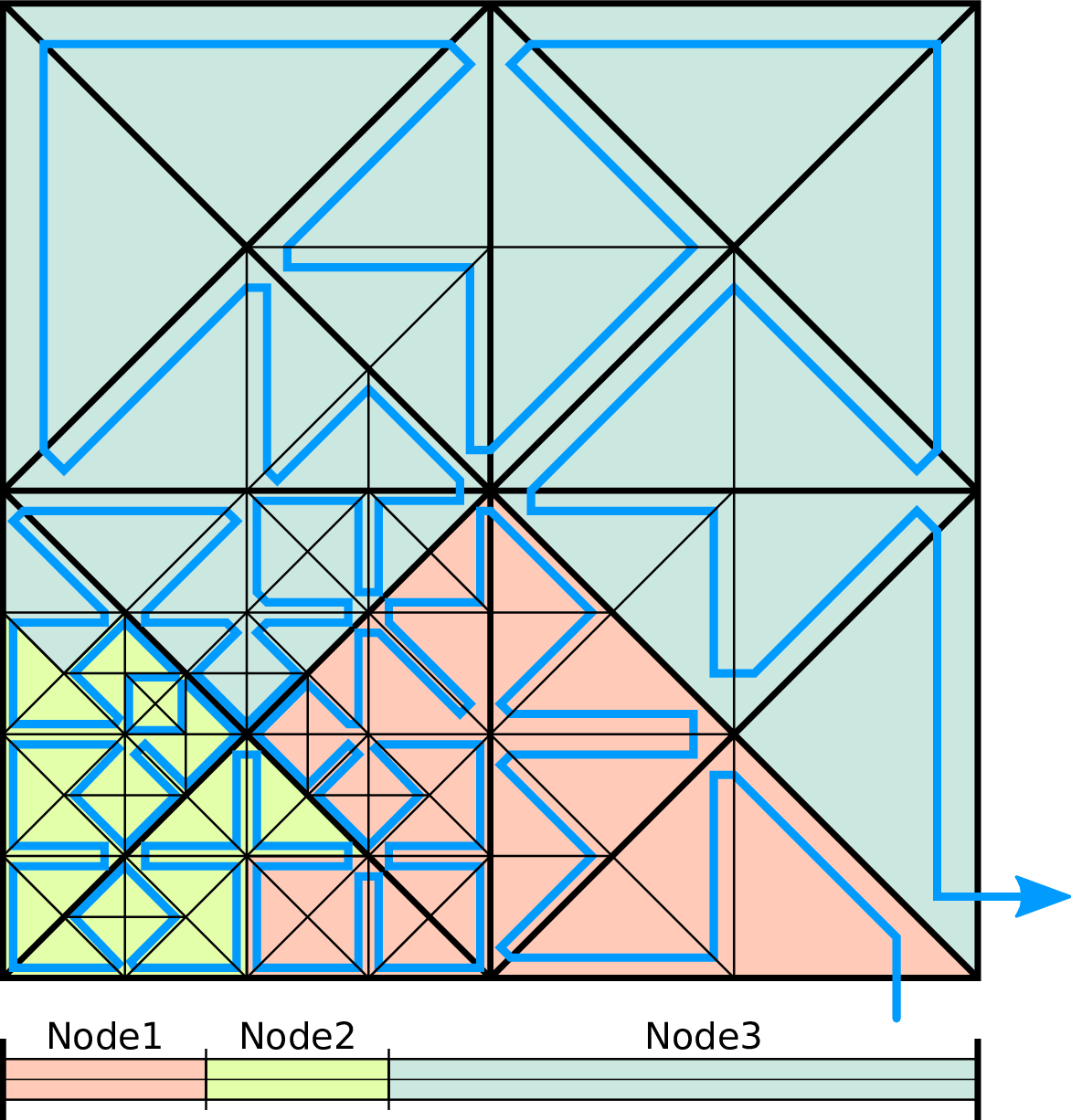
We start with an SFC-based domain decomposition of a discretized domain Ω_d = ⋃ _i{C_i} with cells C_i. By ordering and enumerating all cells along the SFC, a partitioning into N non-overlapping partitions P_k ∈ Ω_d with 1 ≤ k ≤ N can be achieved: This associates cells to a partition k by generating an interval for each partition with the start cell id S_k and an end id given by the next partition’s cell start id S_k+1,

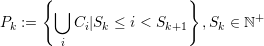
{ } ⋃ Pk := Ci|Sk ≤ i < Sk+1 ,Sk ∈ ℕ+ i

with S_N+1 := |C| + 1. The communication interfaces

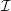between two different partitions P_i and P_j with i≠j are given by a set of hyperfaces

Ii,j := {Pi ∩ Pj}.

We further refer to hyperfaces created by the Sierpiński SFC to be edges (hyperfaces of dimension d - 1) and nodes (hyperfaces of dimension d - 2).

With the spacetree-based grid greneration inducing a serialization of the underlying grid cells with the SFC, there are two common ways on partitioning such a grid:

pict

Figure 5.1: Domain partitioning with SFC cuts. Top image: 2D Sierpinski partitioning with each partition given in a different color. Bottom image: 1D representation of the partitioning, each interval representing a partition.

pict

Figure 5.2: Partitioning of a triangular-shaped domain partitioning with tree splits. Left image: domain triangulation with each partition marked with a thick red border. Right image: representation of the tree split domain partitioning with the refinement tree. The triangle nodes represent the cells, the gray-filled circles the subtree’s root node.

SFC cuts:
With SFC cuts [Beh05,DBH⁺05], partitions are generated by cutting the one-dimensional representation of the SFC into equally sized chunks. This aims at improving the load balancing by cutting the SFC at appropriate positions. An example of generated partitions based on the Sierpiński SFC is given in Fig. 5.1.
Tree splits:
With the grid generation based on the recursively defined spacetree, we can generate partitions by using the naturally given bisection. A partitioning is then based on tree splits (see also [Wei09]) with cells represented by leaf nodes of subtrees, see Fig. 5.2. These subtrees are a special case of the SFC cuts.

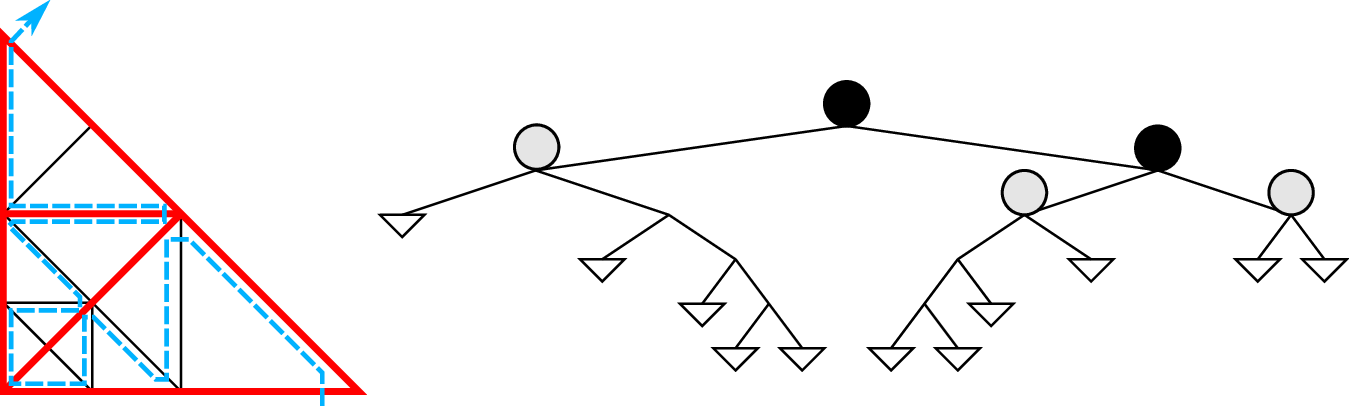
The communication, data migration and code-generator-based optimizations (see Sec. 4.10.1) which we derive in this thesis can be applied to spacetree splits and also SFC cuts. Due to historical reasons and the existing code generator for recursive traversals of subtrees, we decided to continue with the parallelization based on the tree splits.

5.1.2 Shared- and replicated-data scheme

We distinguish between parallelization approaches by considering methods with shared and replicated parallelization [SWB13b] ¹ . Both methods are based on a domain decomposition into multiple partitions, each partition sharing hyperfaces of dimension d - 1 or less with adjacent partitions. We refer to these shared hyperfaces as shared interfaces dP_k. With each compute unit executing operations and modifying data associated on each partition in parallel, data on these shared interfaces is accessed in parallel and has to be kept consistent. Based on our grid generated with a spacetree, we consider two different data access schemes, each one resulting in a different parallelization approach:

Shared data scheme (shared access synchronization):
The SFC induces a serialization of the domain data into a stream. With a shared data scheme following the SFC input stream, multiple compute units can operate on the same input data stream, but on different chunks of the input stream. Due to accessing the same data, an access synchronization to avoid race conditions is required. This would lead to a parallelization approach that requires frequent access synchronizations using e.g. mutices, or spin locks.
Replicated data scheme (replicated data synchronization):
Using a replicated data scheme, the data on shared interfaces is considered to be replicated. This leads to a parallelization approach with computations on each partition executed massively in parallel without any synchronization, followed by data synchronization, e.g. a reduce operation on the replicated data on the shared interfaces (see [Vig12]).

The replicated data scheme with separated data buffers (stacks and streams, e.g.) for each partition is typically used for distributed-memory environments since replicated data can be sent and reduced after the receive operation by using distributed-memory messaging. For shared-memory environments, such communication interfaces are typically not available or, lead to additional overhead. In this work, we developed a run-length encoding of meta information to make the replicated data scheme also feasible on shared-memory systems (see Section 5.2). Our method does not only avoid these overheads for shared-memory systems, but also leads to an elegant solution for distributed-memory parallelization. We continue to use the replicated-data scheme in the present work.

5.1.3 Partition scheduling

Once the partitions are generated, several scheduling possibilities exist to assign computations on SFC-based domain partitions to compute units.

1:1 scheduling:
With a 1:1 assignment of partitions to compute units, each partition of the domain is assigned to a single compute unit. We refer to this as a 1:1 scheduling. Using a stack- and stream-based communication scheme, this approach was taken so far for SFC cuts with the Sierpiński SFC (see e.g. [Vig12]) as well as tree splits with the Peano SFC [Wei09] for distributed memory only, both assigning a compute unit to a single partition.
N:1 scheduling:
With a partitioning approach based on tree splits, a 1:1 scheduling approach would clearly lead to high idle times due to workload imbalances (left image in Fig. 5.3). An alternative to this approach is massive splitting [SBB12] creating by far more subtree-oriented partitions than there are compute units available, resulting in an N:1 scheduling (right image in Fig. 5.3).

pict

Figure 5.3: 1:1 (left) vs. N:1 (right) scheduling with partitions generated by subtrees. Each yellow block is representative for a single grid cell. The blocks in dark-yellow color represent execution overheads to run computations on a partition. The N:1 scheduling leads to less idle time for typical grid structures of dynamically changing grids [SBB12].

For SFC-cuts, a 1:1 partition scheduling allows an optimized implementation due to avoiding object-oriented overheads with single-threaded MPI (cf. [Vig12]). With the focus of our partition generation based on tree splits, such a 1:1 scheduling would lead to the above mentioned load imalances. Therefore, an N:1 scheduling as well as an object-oriented software approach gets mandatory to tackle the N:1 load balancing.

[next] [front] [up]